【题目】在ABCD中，点E、F分别在AB、CD上，且AE=CF．
（1）求证：△ADE≌△CBF；
（2）若DF=BF，求证：四边形DEBF为菱形．
【答案】(1)证明过程见解析；(2)证明过程见解析
【解析】
试题分析：(1)、首先根据平行四边形的性质可得AD=BC，∠A=∠C，再加上条件AE=CF可利用SAS证明三角形全等；(2)、首先根据AE=CF得出DF=BE，再加上条件AB∥CD可得四边形DEBF是平行四边形，再根据DF=FB，可根据邻边相等的平行四边形为菱形证出结论．
试题解析：(1)、∵四边形ABCD是平行四边形， ∴AD=BC，∠A=∠C，
∵在△ADE和△CBF中，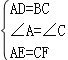
， ∴△ADE≌△CBF（SAS）；
(2)、∵四边形ABCD是平行四边形， ∴AB∥CD，AB=CD， ∵AE=CF， ∴DF=EB，
∴四边形DEBF是平行四边形， 又∵DF=FB， ∴四边形DEBF为菱形．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】某厂前年缴税30万元，今年缴税36.3万元，若该厂缴税的年平均增长率为x，则可列方程（ ）
A.30x2=36.3
B.30（1-x）2=36.3
C.30+30（1+x）+30（1+x）2=36.3
D.30（1+x）2=36.3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下表是一组二次函数y=x2+3x﹣5的自变量x与函数值y的对应值：
x | 1 | 1.1 | 1.2 | 1.3 | 1.4 |
y | ﹣1 | ﹣0.49 | 0.04 | 0.59 | 1.16 |
那么方程x2+3x﹣5=0的一个近似根是（ ）
A.1
B.1.1
C.1.2
D.1.3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠MON=90°，点A、B分别在直线OM、ON上，BC是∠ABN的平分线.
（1）如图1,若BC所在直线交∠OAB的平分线于点D时,尝试完成①、②两题：
①当∠ABO＝30°时，∠ADB＝ °
②当点A、B分别在射线OM、ON上运动时（不与点O重合），试问:随着点A、B的运动，∠ADB的大小会变吗？如果不会，请求出∠ADB的度数；如果会，请求出∠ADB的度数的变化范围；
（2）如图2, 若BC所在直线交∠BAM的平分线于点C时,将△ABC沿EF折叠，使点C落在四边形ABEF内点C′的位置.求∠BEC′+∠AFC′ 的度数.
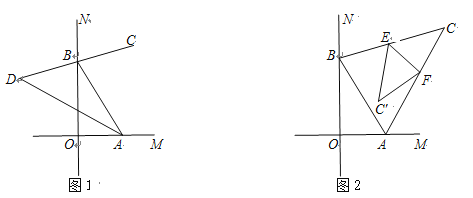
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y＝2x2的图象可以看做抛物线y＝2( x-1）2+3怎样平移得到的（ ）
A.向左平移1个单位，再向下平移3个单位
B.向左平移1个单位，再向上平移3个单位
C.向右平移1个单位，再向上平移3个单位
D.向右平移1个单位，再向下平移3个单位
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一艘渔船位于小岛Ｍ的北偏东45°方向、距离小岛180海里的A处，渔船从A处沿正南方向航行一段距离后，到达位于小岛南偏东60°方向的B处。
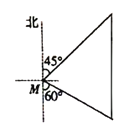
（1）求渔船从A到B的航行过程中与小岛M之间的最小距离（结果用根号表示）：
（2）若渔船以20海里/小时的速度从B沿BM方向行驶，求渔船从B到达小岛M的航行时间（结果精确到0.1小时）。（参考数据：
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把直线y=-x-1沿x轴向右平移2个单位，所得直线的函数解析式为（ ）
A. y=-x+1B. y=-x-3C. y=-2x-1D. y=2x-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com