
【题目】如图,∠MON=90°,点A、B分别在直线OM、ON上,BC是∠ABN的平分线.
(1)如图1,若BC所在直线交∠OAB的平分线于点D时,尝试完成①、②两题:
①当∠ABO=30°时,∠ADB= °
②当点A、B分别在射线OM、ON上运动时(不与点O重合),试问:随着点A、B的运动,∠ADB的大小会变吗?如果不会,请求出∠ADB的度数;如果会,请求出∠ADB的度数的变化范围;
(2)如图2, 若BC所在直线交∠BAM的平分线于点C时,将△ABC沿EF折叠,使点C落在四边形ABEF内点C′的位置.求∠BEC′+∠AFC′ 的度数.
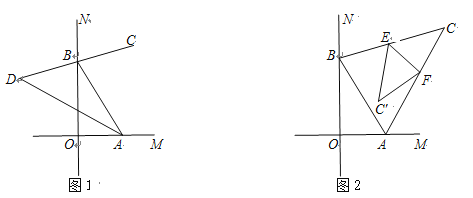
【答案】(1)①45;②∠ADB的大小不会变,为45°;
(2)∠BEC′+∠AFC′ 的度数是90°;
【解析】试题分析: (1) ①根据角平分线的定义可得: ∠NBC=∠ABC,然后根据对顶角相等可得: ∠NBC=∠DBO,然后由已知可得: ∠ABO=30°,然后由三角形外角的性质可得: ∠NBA=∠BOA+∠BAO =120°,进而可得: ∠NBC=∠ABC=60°,然后由AD是∠OAB的平分线得到∠BAD=![]() ∠BAO=15°,最后由∠BAD+∠BDA=∠ABC即可求出答案;
∠BAO=15°,最后由∠BAD+∠BDA=∠ABC即可求出答案;
②∠ADB的大小不随点A,B的移动而发生变化,根据三角形的一个外角等于和它不相邻的两个内角的和, ∠ABN=∠OAB+∠MON, ∠CBA=∠ADB+∠DAB,再根据角平分线的定义∠DAB=![]() ∠OAB, ∠CBA=
∠OAB, ∠CBA=![]() ∠ABN,代入整理即可得到∠ADB=
∠ABN,代入整理即可得到∠ADB=![]() ∠MON=45°.
∠MON=45°.
(2)首先根据已知证出∠C=45°,从而得到∠C EC′+∠CFC′=2(180°-∠C)=270°,进而得到∠BEC′+∠AFC′=360°-(∠C EC′+∠CFC′)=90°。
试题解析:
(1)①45
②设∠ABO=α,
∵∠MON=90°
∴∠BAD=![]() ,∠ABC=
,∠ABC=![]()
∴∠ABD=180°-∠ABC=![]()
∴∠ADB=180°-∠BAD -∠ABD=45°
(2)∵∠MON=90°
∴∠ABO+∠BAO=90°
∴∠CAB+∠CBA=![]() (∠BAM+∠ABN)=135°
(∠BAM+∠ABN)=135°
∴∠C=45°
∴∠C EC′+∠CFC′=2(180°-∠C)=270°
∴∠BEC′+∠AFC′=360°-(∠C EC′+∠CFC′)=90°


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0),B(4,0),C(0,2)三点
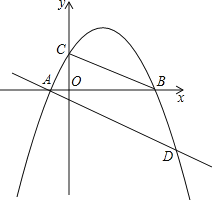
(1)求这条抛物线的解析式;
(2)E为抛物线上一动点,是否存在点E使以A、B、E为顶点的三角形与△COB相似?若存在,试求出点E的坐标;若不存在,请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、A、C在一条直线上,给出下列三个事项:①AD⊥BC, EG⊥BC,垂足分别为D、G;②∠1=∠2;③AD平分∠BAC.

(1)以其中两个事项作为条件,另一个事项作为结论,你能组成 个正确的结论;
(2)请你选择其中一个正确结论进行说明理由.
解:以 为条件, 为结论.(填写序号)
理由是:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C; ②∠AEF=∠AFE; ③∠EBC=∠C;④AG⊥EF.正确结论有( )
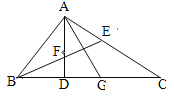
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,点P是三角形右外一点,且∠APB=∠ABC.

(1)如图1,若∠BAC=60°,点P恰巧在∠ABC的平分线上,PA=2,求PB的长;
(2)如图2,若∠BAC=60°,探究PA,PB,PC的数量关系,并证明;
(3)如图3,若∠BAC=120°,请直接写出PA,PB,PC的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com