练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．下列各组数中，不能作为直角三角形的三边长的是（　　）
    A．0.3，0.4，0.5B．8，9，10C．7，24，25D．9，12，15

    分析 由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可．

    解答 解：A、0.32+0.42=0.52，故是直角三角形，故此选项不合题意；
    B、82+92≠102，故不是直角三角形，故此选项符合题意；
    C、72+242=252，故是直角三角形，故此选项不合题意；
    D、92+122=152，故是直角三角形，故此选项不合题意．
    故选B．

    点评 本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．解不等式组：$\left\{\begin{array}{l}x-2≤0\\ 2（x-1）+（3-x）＞0\end{array}\right.$，并把它的解集在数轴上表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，从地面上的点A看一山坡上的电线杆PQ，测得杆顶端点P的仰角是45°，向前走6m到达B点，测得杆顶端点P和杆底端点Q的仰角分别是60°和30°．
    （1）求∠BPQ的度数；
    （2）求该电线杆PQ的高度（结果精确到1m）．
    备用数据：$\sqrt{3}≈1.7$，$\sqrt{2}≈1.4$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知y＜$\sqrt{x-2}$+$\sqrt{2-x}$+3，化简|y-3|-$\sqrt{{y}^{2}-8y+16}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．在代数式$\frac{a}{3}$、$\frac{x}{x+1}$、$\frac{1}{5}$x+y、$\frac{{a}^{2}-{b}^{2}}{a-b}$，$\frac{3}{π}$中分式有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．计算
    （1）（3$\sqrt{12}$-2$\sqrt{\frac{1}{3}}$+$\sqrt{48}$）÷2$\sqrt{3}$
    （2）$\frac{3}{\sqrt{3}}$-（$\sqrt{3}$）2+（π+$\sqrt{3}$）0-$\sqrt{27}$+|$\sqrt{3}$-2|
    （3）（2$\sqrt{5}$+$\sqrt{3}$）2-（$\sqrt{5}$+$\sqrt{2}$）（$\sqrt{5}$-$\sqrt{2}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知x+y=3，xy=2，求x2+y2，x-y的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．以下两题任选其一作答：
    （1）如图，在方格纸中（小正方形的边长为1），△ABC的三个顶点均为格点，将△ABC沿x轴向左平移5个单位长度，根据所给的直角坐标系（O是坐标原点），
    解答下列问题：①画出平移后的△A′B′C′．②直接写出点A′、B′、C′的坐标．
    （2）一个正数x的平方根是2a-4与6-a，求a和x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

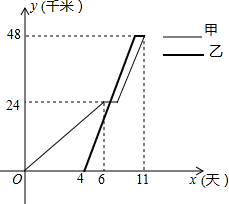    19．甲、乙两工程队维修同样长度的两段公路，甲队每天完成a千米，中间因故停工一段时间，之后又以每天2a千米的速度继续工作；乙队在甲队工作4天后开始工作，比甲队早一天完成任务．设甲、乙两工程队各自完成任务的工作量为y（千米），甲队的工作时间为x（天）．当0≤x≤11时，y与x之间的函数图象如图所示．
    （1）求a的值．
    （2）求甲队因故停工的时间．
    （3）求乙工程队进行维修期间完成的工作量y与x之间的函数关系式．
    （4）设甲、乙两队工作量的差为p千米，当0＜p≤8时，x的取值范围是0＜x≤2，6≤x＜7，7＜x＜11．

    查看答案和解析>>

    同步练习册答案