
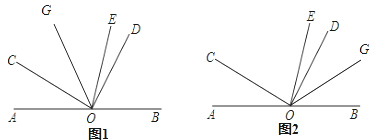
【题目】如图,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.

(1)若∠AOC=30°,求∠DOE的度数;
(2)若∠AOC=α,直接写出∠DOE的度数(用含α的代数式表示);
(3)在(1)的条件下,∠BOC的内部有一射线OG,射线OG将∠BOC分为1:4两部分,求∠DOG的度数.
【答案】(1)15°(2)![]() α(3)①60°②30°
α(3)①60°②30°
【解析】
(1)由已知可求出∠BOD=180°-90°-30°=60°,再由∠COB是150°,OE平分∠BOC求出∠DOE的度数;(2)根据(1)的解题思路,可求出∠DOE的度数;(3) ∠BOC的内部有有一射线OG,射线OG将∠BOC分为1:4两部分,题中没有明确射线OG的位置,分情况解答即可.
(1)∵∠COD是直角,∠AOC=30°,
∴∠BOD=180°﹣90°﹣30°=60°,
∴∠COB=90°+60°=150°,
∵OE平分∠BOC,
∴∠BOE=![]() ∠BOC=75°,
∠BOC=75°,
∴∠DOE=∠BOE﹣∠BOD=75°﹣60°=15°.
(2)∵∠COD是直角,∠AOC=α,
∴∠BOD=180°﹣90°﹣α=90°﹣α,
∴∠COB=90°+90°﹣α=180°﹣α,
∵OE平分∠BOC,
∴∠BOE=![]() ∠BOC=90°﹣
∠BOC=90°﹣![]() α,
α,
∴∠DOE=∠BOE﹣∠BOD=90°﹣![]() α﹣(90°﹣α)=
α﹣(90°﹣α)=![]() α.
α.
(3)①当射线OG位于DC之间时,如图1所示
∵∠AOC=30°,射线OG将∠BOC分为1:4两部分,
∴∠BOC=150°,∠COG=30°,∠BOG=120°
由(1)知:∠BOD=60°,
∴∠DOG=∠BOG﹣∠BOD=120°﹣60°=60°
②当射线OG位于DB之间时,如图2所示
∵∠AOC=30°,射线OG将∠BOC分为1:4两部分,
∴∠BOC=150°,∠COG=120°,∠BOG=30°
由(1)知:∠BOD=60°,
∴∠DOG=∠BOD﹣∠BOG=60°﹣30°=30°


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某中学的高中部在A校区,初中部在B校区,学校学生会计划在3月12日植树节当天安排部分学生到郊区公园参加植树活动.已知A校区的每位高中学生往返车费是6元,B校区的每位初中学生往返的车费是10元,要求初、高中均有学生参加,且参加活动的初中学生比参加活动的高中学生多4人,本次活动的往返车费总和不超过210元,求初、高中最多各有多少学生参加.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABD是边长为3的等边三角形,E,F分别是边AD,AB上的动点,若∠ADC=∠ABC=90°,则△CEF周长的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个正方体的平面展开图,标注了A字母的是正方体的正面,如果正方体的左面与右面标注的式子相等.

(1)求x的值.
(2)求正方体的上面和底面的数字和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB,点P是∠AOB内部的一个定点,点E、F分别是OA、OB上的动点.
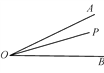
(1)要使得△PEF的周长最小,试在图上确定点E、F的位置.
(2)若OP=4,要使得△PEF的周长的最小值为4,则∠AOB=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AB=CD,M、N分别是AD和BC的中点,延长BA和CD分别交射线NM于点E和点F,若tan∠F=![]() , FC=FN,EN=
, FC=FN,EN=![]() , 则EF=
, 则EF= 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在菱形ABCD中,∠ADC=60°,点H为CD上任意一点(不与C、D重合),过点H作CD的垂线,交BD于点E,连接AE.
(1)如图1,线段EH、CH、AE之间的数量关系是;
(2)如图2,将△DHE绕点D顺时针旋转,当点E、H、C在一条直线上时,求证:AE+EH=CH
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图某超市举行“翻牌”抽奖活动,在一张木板上共有6个相同的牌,其分别对应价值为2元、5元、8元、10元、20元和50元的奖品.
(1)小雷在该抽奖活动中随机翻一张牌,求抽中10元奖品的概率;
(2)如果随机翻两张牌,且第一次翻过的牌不再参加下次翻牌,求两次抽中的奖品的总价值大于14元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点A(﹣1,t),B(3,t),与y轴交于点C(0,﹣1).一次函数y=x+n的图象经过抛物线的顶点D.
(1)求抛物线的表达式;
(2)求一次函数y=x+n的表达式;
(3)将直线l:y=mx+n绕其与y轴的交点E旋转,使当﹣1≤x≤1时,直线l总位于抛物线的下方,请结合函数图象,求m的取值范围.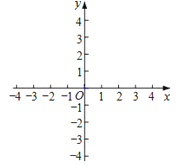
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com