
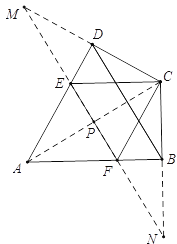
【题目】如图,△ABD是边长为3的等边三角形,E,F分别是边AD,AB上的动点,若∠ADC=∠ABC=90°,则△CEF周长的最小值为______.

【答案】6
【解析】如图,因为![]() ,所以分别作点C关于AD、AB的对称点M、N,连接MN,MN与AD交于点E,与AB交于点F,连接CE、CF,则此时△CEF的周长最小,
,所以分别作点C关于AD、AB的对称点M、N,连接MN,MN与AD交于点E,与AB交于点F,连接CE、CF,则此时△CEF的周长最小,
连接AC,交MN于点P,
由作图可知CE=ME、CF=FN,∴△CEF的周长:CE+CF+EF=MN,
∵△ABD是等边三角形,∴AB=AD=3,∠DAB=∠ADB=∠ABD=60°,
∵∠ADC=∠ABC=90°,∴∠CDB=∠CBD=30°,
∴CD=CB,
∵DM=CD,BN=CB,∴CM=2CD=2BC=CN,MN//BD,∴∠M=∠N=∠CDB=30°,
又∵AC=AC,∴△ADC≌△ABC,
∴CD=CB,∠DAC=∠BAC=![]() ∠DAB=30°,
∠DAB=30°,
∴AC=2CD,∠M=∠DAC,∴AC=CM,
又∵∠ACD=∠MCP,∴△ACD≌△MCP,∴MP=AD=3,∠MPC=∠ADC=90°,
∴MN=2MP=6,
即△CEF周长的最小值是6,
故答案为:6.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△CDE的顶点C点坐标为C(1,﹣2),点D的横坐标为![]() , 将△CDE绕点C旋转到△CBO,点D的对应点B在x轴的另一个交点为点A.
, 将△CDE绕点C旋转到△CBO,点D的对应点B在x轴的另一个交点为点A.
(1)图中,∠OCE等于多少;
(2)求抛物线的解析式;
(3)抛物线上是否存在点P,使S△PAE=![]() S△CDE?若存在,直接写出点P的坐标;若不存在,请说明理由.
S△CDE?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A,B,C,D四个点,且2AB=BC=3CD,若A,D两点表示的数分别为-5,6,点E为BD的中点,则该数轴上点E表示的数是____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“1”和“4”(单位:cm),则该圆的半径为( )
A.5cm
B.![]() cm
cm
C.![]() cm
cm
D.![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有2个红球(记为红球1、红球2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是多少;
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表),求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校刚完成一批结构相同的学生宿舍的修建,这些宿舍地板需要铺瓷砖,一天4名一级技工去铺4个宿舍,结果还剩12 m2地面未铺瓷砖;同样时间内6名二级技工铺4个宿舍刚好完成,已知每名一级技工比二级技工一天多铺3 m2瓷砖.
(1)求每个宿舍需要铺瓷砖的地板面积.
(2)现该学校有20个宿舍的地板和36 m2的走廊需要铺瓷砖,某工程队有4名一级技工和6名二级技工,一开始有4名一级技工来铺瓷砖,3天后,学校根据实际情况要求2天后必须完成剩余的任务,所以决定加入一批二级技工一起工作,问需要再安排多少名二级技工才能按时完成任务
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.

(1)若∠AOC=30°,求∠DOE的度数;
(2)若∠AOC=α,直接写出∠DOE的度数(用含α的代数式表示);
(3)在(1)的条件下,∠BOC的内部有一射线OG,射线OG将∠BOC分为1:4两部分,求∠DOG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点C在线段AB上,AC = 8 cm,CB = 6 cm,点M、N分别是AC、BC的中点.
![]()
(1)求线段MN的长.
(2)若C为线段AB上任意一点,满足AC+CB=a(cm),其他条件不变,你能猜想出MN的长度吗?并说明理由.
(3)若C在线段AB的延长线上,且满足AC-CB=b(cm),M、N分别为AC、BC的中点,你能猜想出MN的长度吗?请画出图形,写出你的结论,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com