[题目]如图,在数轴上有A,B,C,D四个点,且2AB=BC=3CD,若A,D两点表示的数分别为-5,6,点E为BD的中点,则该数轴上点E表示的数是 . 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图,在数轴上有A,B,C,D四个点,且2AB=BC=3CD,若A,D两点表示的数分别为-5,6,点E为BD的中点,则该数轴上点E表示的数是____.

【答案】2

【解析】

由A与D表示的数求出AD的长，再根据已知等式用AB，CD表示出BC，根据AB+BC+CD=AD求出BC的长，进而求出AB与CD的长，即可得出该数轴上点E表示的数．

解：∵A、D两点表示的数分别为-5和6，

∴AD=11，

∵BC=2AB=3CD，

∴AB=BC，CD=BC，

∴AD=AB+BC+CD=11，即BC+BC+BC=11，

∴BC=6，AB=3，CD=2，

则B、D两点所表示的数分别为-2和6，

该数轴上点E表示的数是（-2+6）÷2=2．

故答案为：2．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】下列结论：

①若a＋b＋c＝0，且abc≠0，则；

②若a＋b＋c＝0，且a≠0，则x＝1一定是方程ax＋b＋c＝0的解；

③若a＋b＋c＝0，且abc≠0，则abc＞0；

④若|a|>|b|，则>0.

其中正确的结论是(　　)

A. ①②③ B. ①②④ C. ②③④ D. ①②③④

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在△ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．

（1）如图1，当点D在线段BC上，如果∠BAC=90°，则∠BCE=　　度；

（2）设∠BAC=α，∠BCE=β．

①如图2，当点D在线段BC上移动，则α，β之间有怎样的数量关系？请说明理由；

②当点D在直线BC上移动，则α，β之间有怎样的数量关系？请直接写出你的结论．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某中学的高中部在A校区，初中部在B校区，学校学生会计划在3月12日植树节当天安排部分学生到郊区公园参加植树活动．已知A校区的每位高中学生往返车费是6元，B校区的每位初中学生往返的车费是10元，要求初、高中均有学生参加，且参加活动的初中学生比参加活动的高中学生多4人，本次活动的往返车费总和不超过210元，求初、高中最多各有多少学生参加．

查看答案和解析>>

科目：初中数学 来源： 题型：

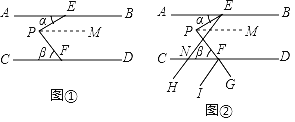
【题目】如图①，已知AB∥CD，点E、F分别是AB、CD上的点，点P是两平行线之间的一点，设∠AEP=α，∠PFC=β，在图①中，过点E作射线EH交CD于点N，作射线FI，延长PF到G，使得PE、FG分别平分∠AEH、∠DFl，得到图②．

（1）在图①中，过点P作PM∥AB，当α=20°，β=50°时，∠EPM=　　度，∠EPF=　　度；

（2）在（1）的条件下，求图②中∠END与∠CFI的度数；

（3）在图②中，当FI∥EH时，请直接写出α与β的数量关系．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】今年以来，国务院连续发布了《关于加快构建大众创业万众创新支撑平台的指导意见》等一系列支持性政策，各地政府高度重视、积极响应，中国掀起了大众创业万众创新的新浪潮．某创新公司生产营销A、B两种新产品，根据市场调研，发现如下信息：
信息1：销售A种产品所获利润y（万元）与所售产品x（吨）之间存在二次函数关系y=ax2+bx，当x=1时，y=7；当x=2时，y=12．
信息2：销售B种产品所获利润y（万元）与所售产品x（吨）之间存在正比例函数关系y=2x．
根据以上信息，解答下列问题：
（1）求a，b的值；
（2）该公司准备生产营销A、B两种产品共10吨，请设计一个生产方案，使销售A、B两种产品获得的利润之和最大，最大利润是多少？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，OD平分∠BOC，OE平分∠AOC，∠BOC＝60°，∠AOC＝58°.

(1)求出∠AOB及其补角的度数；

(2)①请求出∠DOC和∠AOE的度数；

②判断∠DOE与∠AOB是否互补，并说明理由．