
【题目】如图,OD平分∠BOC,OE平分∠AOC,∠BOC=60°,∠AOC=58°.
(1)求出∠AOB及其补角的度数;
(2)①请求出∠DOC和∠AOE的度数;
②判断∠DOE与∠AOB是否互补,并说明理由.

【答案】(1)118°;62°(2)①29°②不互补
【解析】
(1)由∠AOB=∠BOC+∠AOC可求出∠AOB的度数,进而求出其补角的度数.
(2)①由OD和OE是∠BOC和∠AOC的平分线可求出∠DOC和∠AOE的度数.
②由∠DOE=∠DOC+∠COE可知∠DOE的度数,计算∠AOB与∠DOE的和即可判断∠AOB与∠DOE是否为补角.
(1)∠AOB=∠BOC+∠AOC=60°+58°=118°,
其补角为180°-∠AOB=180°-118°=62°.
(2)①因为OD平分∠BOC,OE平分∠AOC,
所以∠DOC=∠BOD=![]() ∠BOC=
∠BOC=![]() ×60°=30°,∠AOE=∠COE=
×60°=30°,∠AOE=∠COE=![]() ∠AOC=
∠AOC=![]() ×58°=29°.
×58°=29°.
②∠DOE与∠AOB不互补.
理由:因为∠DOC=30°,∠COE=29°,
所以∠DOE=∠DOC+∠COE=59°.
所以∠DOE+∠AOB=59°+118°=177°,![]()
故∠DOE与∠AOB不互补.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与线段AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠AOF的度数是( )
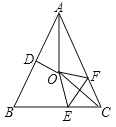
A.105° B.110° C.115° D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
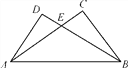
【题目】如图,在△ABC和△BAD中,AC与BD相交于点E,已知AD=BC,另外只能从下面给出的三个条件:①∠DAB=∠CBA;②∠D=∠C;③∠DBA=∠CAB中选择其中的一个用来证明△ABC和△BAD全等,这个条件是 (填序号),并证明△ABC≌△BAD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A,B,C,D四个点,且2AB=BC=3CD,若A,D两点表示的数分别为-5,6,点E为BD的中点,则该数轴上点E表示的数是____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,5AO=3CO.
(1)写出数轴上点A、C表示的数;
(2)点P、Q分别从A、C同时出发,点P以每秒2个单位长度的速度沿数轴向右匀速运动,点Q以每秒6个单位长度的速度沿数轴向左匀速运动,M为线段AP的中点,点N在线段CQ上,且CN=![]() CQ.设运动的时间为t(t>0)秒.
CQ.设运动的时间为t(t>0)秒.
①数轴上点M、N表示的数分别是 (用含t的式子表示);
②t为何值时,M、N两点到原点的距离相等?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“1”和“4”(单位:cm),则该圆的半径为( )
A.5cm
B.![]() cm
cm
C.![]() cm
cm
D.![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校刚完成一批结构相同的学生宿舍的修建,这些宿舍地板需要铺瓷砖,一天4名一级技工去铺4个宿舍,结果还剩12 m2地面未铺瓷砖;同样时间内6名二级技工铺4个宿舍刚好完成,已知每名一级技工比二级技工一天多铺3 m2瓷砖.
(1)求每个宿舍需要铺瓷砖的地板面积.
(2)现该学校有20个宿舍的地板和36 m2的走廊需要铺瓷砖,某工程队有4名一级技工和6名二级技工,一开始有4名一级技工来铺瓷砖,3天后,学校根据实际情况要求2天后必须完成剩余的任务,所以决定加入一批二级技工一起工作,问需要再安排多少名二级技工才能按时完成任务
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿数轴做如下移动:第一次将点A向左移动3个单位长度到达点A1,第2次将点A1向右平移6个单位长度到达点A2,第3次将点A2向左移动9个单位长度到达点A3…则第6次移动到点A6时,点A6在数轴上对应的实数是_____;按照这种规律移动下去,第2017次移动到点A2017时,A2017在数轴上对应的实数是__________.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com