
【题目】某学校刚完成一批结构相同的学生宿舍的修建,这些宿舍地板需要铺瓷砖,一天4名一级技工去铺4个宿舍,结果还剩12 m2地面未铺瓷砖;同样时间内6名二级技工铺4个宿舍刚好完成,已知每名一级技工比二级技工一天多铺3 m2瓷砖.
(1)求每个宿舍需要铺瓷砖的地板面积.
(2)现该学校有20个宿舍的地板和36 m2的走廊需要铺瓷砖,某工程队有4名一级技工和6名二级技工,一开始有4名一级技工来铺瓷砖,3天后,学校根据实际情况要求2天后必须完成剩余的任务,所以决定加入一批二级技工一起工作,问需要再安排多少名二级技工才能按时完成任务
【答案】(1)每个宿舍需要铺瓷砖的地板面积为18 m2;(2)需要再安排4名二级技工才能按时完成任务.
【解析】
(1)设每个宿舍需要铺瓷砖的地板面积为xm2,根据每名一级技工比二级技工一天多铺3m2瓷砖列出方程,然后求解即可;
(2)设需要再安排y名二级技工才能按时完成任务,根据每名一级技工每天可铺砖面积和每名二级技工每天可铺砖面积列出方程,然后求解即可得出答案.
(1)设每个宿舍需要铺瓷砖的地板面积为x m2,则依题意列出方程:
![]() -
-![]() =3,
=3,
解方程得:x=18.
所以每个宿舍需要铺瓷砖的地板面积为18 m2.
(2)设需要再安排y名二级技工才能按时完成任务.
因为每名一级技工每天可铺砖面积:![]() =15(m2),
=15(m2),
每名二级技工每天可铺砖面积:15-3=12(m2),
所以15×4×5+2×12y=20×18+36.
解得:y=4.
所以需要再安排4名二级技工才能按时完成任务.


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE= 度;
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OD平分∠BOC,OE平分∠AOC,∠BOC=60°,∠AOC=58°.
(1)求出∠AOB及其补角的度数;
(2)①请求出∠DOC和∠AOE的度数;
②判断∠DOE与∠AOB是否互补,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABD是边长为3的等边三角形,E,F分别是边AD,AB上的动点,若∠ADC=∠ABC=90°,则△CEF周长的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.
(1)求证:ED∥AC;
(2)连接AE,试证明:ABCD=AEAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个正方体的平面展开图,标注了A字母的是正方体的正面,如果正方体的左面与右面标注的式子相等.

(1)求x的值.
(2)求正方体的上面和底面的数字和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB,点P是∠AOB内部的一个定点,点E、F分别是OA、OB上的动点.
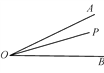
(1)要使得△PEF的周长最小,试在图上确定点E、F的位置.
(2)若OP=4,要使得△PEF的周长的最小值为4,则∠AOB=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在菱形ABCD中,∠ADC=60°,点H为CD上任意一点(不与C、D重合),过点H作CD的垂线,交BD于点E,连接AE.
(1)如图1,线段EH、CH、AE之间的数量关系是;
(2)如图2,将△DHE绕点D顺时针旋转,当点E、H、C在一条直线上时,求证:AE+EH=CH
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中不一定成立的是( )

A. S△BEC=2S△CEF B. EF=CF
C. ∠DCF=![]() ∠BCD D. ∠DFE=3∠AEF
∠BCD D. ∠DFE=3∠AEF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com