
| A. | 5 | B. | -5 | C. | 3 | D. | -3 |
分析 首先根据题意,把x=3代入分式方程$\frac{a-2}{x}$-$\frac{1}{x-2}$=0,然后根据一元一次方程的解法,求出a的值是多少即可.
解答 解:∵x=3是分式方程$\frac{a-2}{x}$-$\frac{1}{x-2}$=0的根,
∴$\frac{a-2}{3}-\frac{1}{3-2}=0$,
∴$\frac{a-2}{3}=1$,
∴a-2=3,
∴a=5,
即a的值是5.
故选:A.
点评 (1)此题主要考查了分式方程的解,要熟练掌握,解答此题的关键是要明确:在解方程的过程中因为在把分式方程化为整式方程的过程中,扩大了未知数的取值范围,可能产生增根,增根是令分母等于0的值,不是原分式方程的解.
(2)此题还考查了一元一次方程的求解方法,要熟练掌握.


科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的边长为4,E为BC上一点,BE=1,F为AB上一点,AF=2,P为AC上一点,则PF+PE的最小值为$\sqrt{17}$.
如图,正方形ABCD的边长为4,E为BC上一点,BE=1,F为AB上一点,AF=2,P为AC上一点,则PF+PE的最小值为$\sqrt{17}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为$\widehat{AB}$的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为($\frac{1}{2}$π+$\frac{\sqrt{2}}{2}$-$\frac{1}{2}$)cm2.
如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为$\widehat{AB}$的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为($\frac{1}{2}$π+$\frac{\sqrt{2}}{2}$-$\frac{1}{2}$)cm2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 50元,30元 | B. | 50元,40元 | C. | 50元,50元 | D. | 55元,50元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
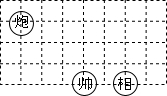 如图所示,这是象棋盘的一部分,若“帅”位于点(-1,-2)上,“相”位于点(1,-2)上,则“炮”位于点( )
如图所示,这是象棋盘的一部分,若“帅”位于点(-1,-2)上,“相”位于点(1,-2)上,则“炮”位于点( )| A. | (-3,1) | B. | (-1,2) | C. | (-4,1) | D. | (-4,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com