
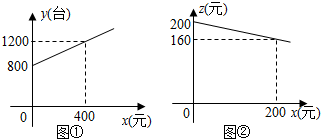
 为了扩大内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定对购买彩电的农户实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图①所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益z(元)会相应降低且z与x之间也大致满足如图②所示的一次函数关系.
为了扩大内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定对购买彩电的农户实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图①所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益z(元)会相应降低且z与x之间也大致满足如图②所示的一次函数关系.分析 (1)根据总收益=每台收益×总台数计算;
(2)结合图象信息分别利用待定系数法求解;
(3)把y与z的表达式代入进行整理,求函数最值.
解答 解:(1)该商场销售家电的总收益为800×200=160000(元);
(2)根据题意设y=k1x+800,Z=k2x+200
∴400k1+800=1200,200k2+200=160
解得k1=1,k2=-$\frac{1}{5}$
∴y=x+800,Z=-$\frac{1}{5}$x+200;
(3)W=yZ=(x+800)•(-$\frac{1}{5}$x+200)=-$\frac{1}{5}$x2+40x+160000=-$\frac{1}{5}$(x-100)2+162000.
∵-$\frac{1}{5}$<0,
∴W有最大值.
当x=100时,W最大=162000
∴政府应将每台补贴款额x定为100元,总收益有最大值,其最大值为162000元.
点评 本题主要考查待定系数法求函数解析式和二次函数的最值问题,审清题意列出代数式是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
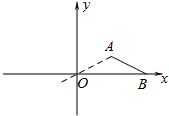 如图,直角坐标系中,线段AB两端点坐标分别为A(4,2)、B(8,0),以原点O为位似中心,将线段AB缩小后得到对应线段A1B1,若B1的坐标为(-4,0),则A1的坐标为( )
如图,直角坐标系中,线段AB两端点坐标分别为A(4,2)、B(8,0),以原点O为位似中心,将线段AB缩小后得到对应线段A1B1,若B1的坐标为(-4,0),则A1的坐标为( )| A. | (2,1) | B. | (-2,-1) | C. | (-1,2) | D. | (-4,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com