
����Ŀ�������κ���y=ax2+bx+c��a��0����ͼ����x��Ľ�������ֱ�Ϊ��x1 �� 0������x2 �� 0������x1��x2 �� ͼ������һ��M��x0 �� y0����x���·�����������˵���� ��b2��4ac��0��
��x=x0�Ƿ���ax2+bx+c=y0�Ľ⣻
��x1��x0��x2
��a��x0��x1����x0��x2����0��
��x0��x1��x0��x2 ��
������ȷ���У� ��
A.�٢�
B.�٢ڢ�
C.�٢ڢ�
D.�٢ڢܢ�
���𰸡�B
���������⣺�١߶��κ���y=ax2+bx+c��a��0����ͼ����x��Ľ�������ֱ�Ϊ��x1 �� 0������x2 �� 0������x1��x2 �� ���ax2+bx+c=0����������ȵ�ʵ������
���=b2��4ac��0������ȷ���ڡ�ͼ������һ��M��x0 �� y0����
��a ![]() +bx0+c=y0 ��
+bx0+c=y0 ��
��x=x0�Ƿ���ax2+bx+c=y0�Ľ⣬����ȷ���۵�a��0ʱ����M��x0 �� y0����x���·���
��x1��x0��x2��
��a��0ʱ����M��x0 �� y0����x���·���
��x0��x1��x0��x2 �� �۴��ܡ߶��κ���y=ax2+bx+c��a��0����ͼ����x��Ľ�������ֱ�Ϊ��x1 �� 0������x2 �� 0����
��y=ax2+bx+c=a��x��x1����x��x2����
��ͼ������һ��M��x0 �� y0����x���·���
��y0=a��x0��x1����x0��x2����0������ȷ���ݸ��ݢۼ��ɵó��ݴ���
���Ͽ�֪��ȷ�Ľ����Т٢ڢܣ�
��ѡB��
�����㾫����������Ĺؼ�����������κ���ͼ���Լ�ϵ��a��b��c�Ĺ�ϵ�����֪ʶ�����ն��κ���y=ax2+bx+c�У�a��b��c�ĺ��壺a��ʾ���ڷ���a>0ʱ�������߿�������; a<0ʱ�������߿�������b��Գ����йأ��Գ���Ϊx=-b/2a;c��ʾ��������y��Ľ������꣺��0��c�����Լ�����������������Ľ�������⣬�˽�һԪ���η��̵Ľ������Ӧ�Ķ��κ�����ͼ����x��Ľ������꣮���һԪ���η����е�b2-4ac���ڶ��κ����б�ʾͼ����x���Ƿ��н��㣮��b2-4ac>0ʱ��ͼ����x�����������㣻��b2-4ac=0ʱ��ͼ����x����һ�����㣻��b2-4ac<0ʱ��ͼ����x��û�н��㣮


 ��ʱ�ƿ�������ϰϵ�д�
��ʱ�ƿ�������ϰϵ�д� һ��һ��һ��ͨϵ�д�
һ��һ��һ��ͨϵ�д� �㽭֮��ѧҵˮƽ����ϵ�д�
�㽭֮��ѧҵˮƽ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������P����AC��һ���㣨����A��C�غϣ�������P��PE��AB������ΪE������EP�� ![]() �ڵ�F��������C�������ڵ�D��
�ڵ�F��������C�������ڵ�D�� 
��1����֤��DC=DP��
��2����ֱ��AB=12cm����CAB=30�㣬 �ٵ�E�ǰ뾶OA�е�ʱ�����߳�DC=cm��
�ڵ�AE=cmʱ����A��O��C��FΪ������ı��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ڿ����еĴ����ٶ�v(m/s)���¶�T(��)�Ĺ�ϵ���±���
�¶�/�� | 0 | 5 | 10 | 15 | 20 |
�ٶ�v/(m/s) | 331 | 334 | 337 | 340 | 343 |
(1)д���ٶ�v���¶�T֮��Ĺ�ϵʽ��
(2)��T��30��ʱ���������Ĵ����ٶȣ�
(3)�������Ĵ����ٶ�Ϊ346m/sʱ���¶��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������֤�����̲���������
��֪����ͼ����B.E�ֱ���AC��DF�ϣ�AF�ֱ�BD��CE�ڵ�M��N����1=��2����A=��F.
��֤����C=��D.

֤������Ϊ��1=��2(��֪).
������1=��ANC(______)��
����______(��������).
����______��______(ͬλ���������ֱ��ƽ��).
���ԡ�ABD=��C(______).
����Ϊ��A=��F(��֪)��
����______��______(______).
����______(��ֱ��ƽ�����ڴ������).
���ԡ�C=��D(______).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ACD�͡�BCE���ǵ���ֱ�������Σ���ACD����BCE��90�㣬AE��DC��F��BD�ֱ�CE��AE�ڵ�G��H.�Բ²��߶�AE��BD��λ�ú�������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ��ֱ�����ǰ壨��45��ǵ�ֱ�����ǰ�ABC����30��ǵ�ֱ�����ǰ�DCB����ͼʾ��ʽ���ţ�б�߽���ΪO�����AOB���COD�����֮�ȵ��� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�һ����ABA1�У���B=20����AB=A1B����A1B��ȡһ��C���ӳ�AA1��A2��ʹ��A1A2=A1C���õ��ڶ�����A1A2C����A2C��ȡһ��D���ӳ�A1A2��A3��ʹ��A2A3=A2D��^����������������ȥ�����5���������У��Ե�A5Ϊ����ĵǵĶ���Ϊ�� ��
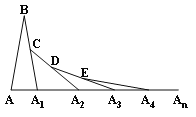
A. 5�� B. 10�� C. 170�� D. 175��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У�AD��BC��AEƽ�֡�BAC��BC�ڵ�E��
��1����B=30�㣬��C=70�������EAD�Ĵ�С��
��2������B����C����2��EAD���C-��B�Ƿ���ȣ�����ȣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Сǿ��С�ն�ס�ڰ���С������ͬһ��ѧУ���飮ij�����ϣ�Сǿ![]() �Ӱ���С��վ����У��ȥѧУ��;����ͣ������վ����ܵ���ѧУվ�㣬��ÿ��վ��ͣ��
�Ӱ���С��վ����У��ȥѧУ��;����ͣ������վ����ܵ���ѧУվ�㣬��ÿ��վ��ͣ��![]() ���ӣ�У����ʻ;��ʼ�ձ������٣��������ϣ�С��
���ӣ�У����ʻ;��ʼ�ձ������٣��������ϣ�С��![]() �Ӱ���С��վ�����������ͬ·�߳��������������ʻ����Сǿ������У����
�Ӱ���С��վ�����������ͬ·�߳��������������ʻ����Сǿ������У����![]() ���ӵ�ѧУվ�㣮���dz����ij����Ӱ���С��վ��������ʻ·��
���ӵ�ѧУվ�㣮���dz����ij����Ӱ���С��վ��������ʻ·��![]() ��ǧ�ף�����ʻʱ��
��ǧ�ף�����ʻʱ��![]() �����ӣ�֮��ĺ���ͼ����ͼ��ʾ��
�����ӣ�֮��ĺ���ͼ����ͼ��ʾ��
��1�����![]() ��������
��������![]() ��ֵ��
��ֵ��
��2��С�ճ���������������ٷ�����Сǿ��������У���������ʱ���Ǿ�ѧУվ���·�̣�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com