
【题目】如图所示是二次函数y=ax2+bx+c(a≠0)图象的一部分,图象过点A(3,0),二次函数图象对称轴为直线x=1,给出四个结论:①b2>4ac;②bc<0;③2a+b=0;④当y>0时,0<x<3.其中正确的结论有( )
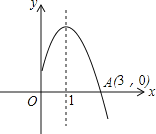
A. 2个 B. 3个 C. 4个 D. 1个
【答案】A
【解析】根据抛物线与x轴的交点个数可判断b24ac>0,即b2>4ac;根据抛物线对称轴为x=![]() =1,由a<0得到b>0,且2a+b=0,再利用抛物线与y轴的交点在x轴上方得到c>0,可判断bc>0;由于抛物线与x轴交于点A(3,0),得到抛物线与x轴的另一个交点为(1,0),所以当1<x<3时,y>0.
=1,由a<0得到b>0,且2a+b=0,再利用抛物线与y轴的交点在x轴上方得到c>0,可判断bc>0;由于抛物线与x轴交于点A(3,0),得到抛物线与x轴的另一个交点为(1,0),所以当1<x<3时,y>0.
∵抛物线与x轴有两个交点,
∴b24ac>0,即b2>4ac,所以①正确;
∵抛物线开口向下,
∴a<0,
∵抛物线对称轴为x=![]() =1,
=1,
∴b>0,2a+b=0,所以③正确;
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴bc>0,所以②错误;
∵抛物线与x轴交于点A(3,0),对称轴为直线x=1,
∴抛物线与x轴的另一个交点为(1,0),
∴当1<x<3时,y>0,所以④错误.
故选:A


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与y轴正半轴相交,其顶点坐标为(
的图象与y轴正半轴相交,其顶点坐标为(![]() ,1),下列结论:①abc>0;②a=b;③a=4c﹣4;④方程
,1),下列结论:①abc>0;②a=b;③a=4c﹣4;④方程![]() 有两个相等的实数根,其中正确的结论是______.(只填序号即可).
有两个相等的实数根,其中正确的结论是______.(只填序号即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
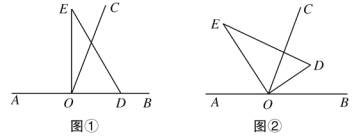
【题目】如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一个直角三角板的直角顶点放在点O处(∠DOE=90°).
(1)如图①,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图②,将直角三角板DOE绕点O转动,若OD恰好平分∠BOC,求∠AOE的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)探索材料1(填空):
数轴上表示数![]() 和数
和数![]() 的两点之间的距离等于
的两点之间的距离等于![]() .例如数轴上表示数2和5的两点距离为
.例如数轴上表示数2和5的两点距离为![]() ;数轴上表示数3和-1的两点距离为
;数轴上表示数3和-1的两点距离为![]() ;则
;则![]() 的意义可理解为数轴上表示数 和 这两点的距离;
的意义可理解为数轴上表示数 和 这两点的距离;![]() 的意义可理解为数轴上表示数 和 这两点的距离;
的意义可理解为数轴上表示数 和 这两点的距离;
(2)探索材料2(填空):
①如图1,在工厂的一条流水线上有两个加工点![]() 和
和![]() ,要在流水线上设一个材料供应点
,要在流水线上设一个材料供应点![]() 往两个加工点输送材料,材料供应点
往两个加工点输送材料,材料供应点![]() 应设在 才能使
应设在 才能使![]() 到
到![]() 的距离与
的距离与![]() 到
到![]() 的距离之和最小?
的距离之和最小?

②如图2,在工厂的一条流水线上有三个加工点![]() 要在流水线上设一个材料供应点
要在流水线上设一个材料供应点![]() 往三个加工点输送材料,材料供应点
往三个加工点输送材料,材料供应点![]() 应设在 才能使
应设在 才能使![]() 到
到![]() 三点的距离之和最小?
三点的距离之和最小?

③如图3,在工厂的一条流水线上有四个加工点![]() ,要在流水线上设一个材料供应点
,要在流水线上设一个材料供应点![]() 往四个加工点输送材料,材料供应点
往四个加工点输送材料,材料供应点![]() 应设在 才能使
应设在 才能使![]() 到
到![]() 四点的距离之和最小?
四点的距离之和最小?

(3)结论应用(填空):
①代数式![]() 的最小值是 ,此时
的最小值是 ,此时![]() 的范围是 ;
的范围是 ;
②代数式![]() 的最小值是 ,此时
的最小值是 ,此时![]() 的值为 .
的值为 .
③代数式![]() 的最小值是 ,此时
的最小值是 ,此时![]() 的范围是 .
的范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=x2-4x+3的图象与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,抛物线的对称轴与x轴交于点D.
(1)求点A,点B和点D的坐标;
(2)在y轴上是否存在一点P,使PBC为等腰三角形?若存在,请求出点P的坐标;
(3)若动点M从点A出发,以每秒1个单位长度的速度沿AB向点B运动,同时另一个动点N从点D出发,以每秒2个单位长度的速度在抛物线的对称轴上运动,当点M到达点B时,点M,N同时停止运动,问点M,N运动到何处时,MNB的面积最大,试求出最大面积.
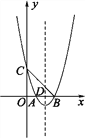
 (备用图)
(备用图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】泉州市某校准备组织教师、学生、家长到福州进行参观学习活动,旅行社代办购买动车票,动车票价格如下表所示:
运行区间 | 大人票价 | 学生票 | ||
出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
泉州 | 福州 | 65(元) | 54(元) | 40(元) |
根据报名总人数,若所有人员都买一等座的动车票,则共需13650元,若都买二等座动车票(学生全部按表中的“学生票二等座”购买),则共需8820元;已知家长的人数是教师的人数的2倍.
(1)设参加活动的老师有m人,请直接用含m的代数式表示教师和家长购买动车票所需的总费用;
(2)求参加活动的总人数;
(3)如果二等座动车票共买到x张,且学生全部按表中的“学生票二等座”购买 ,其余的买一等座动车票,且买票的总费用不低于9000元,求x的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小淇在说明 “直角三角形斜边上的中线等于斜边的一半”是真命题,部分思路如下:如图,在∠ACB内做∠BCD=∠B,CD与AB相交于点D,…….请根据以上思路,完成证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点B的坐标为(6,4).
(1)请用直尺(不带刻度)和圆规作一条直线AC,它与x轴和y轴的正半轴分别交于点A和点C,且使∠ABC=90°,△ABC与△AOC的面积相等.(作图不必写作法,但要保留作图痕迹.)
(2)问:(1)中这样的直线AC是否唯一?若唯一,请说明理由;若不唯一,请在图中画出所有这样的直线AC,并写出与之对应的函数表达式.
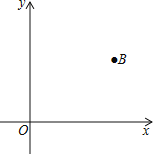
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com