
分析 求得抛物线的顶点坐标为(-m,m2+4m+6),根据根与系数的关系得到α+β=-2m,αβ=-(4m+6),求得抛物线与x轴的两个交点和它的顶点所组成的三角形面积=$\frac{1}{2}$•(m2+4m+6)•2$\sqrt{(m+2)^{2}+2}$=[(m+2)2+2]•$\sqrt{(m+2)^{2}+2}$,于是得到结论.
解答 解:y=-x2-2mx+4m+6=-(x+m)2+m2+4m+6,则抛物线的顶点坐标为(-m,m2+4m+6),
设抛物线与x轴两交点的坐标为(α,0),(β,0),则α、β为方程-x2-2mx+4m+6=0的两实数解,
所以α+β=-2m,αβ=-(4m+6),则|α-β|=$\sqrt{(α+β)^{2}-4αβ}$=$\sqrt{4{m}^{2}+4(4m+6)}$=2$\sqrt{(m+2)^{2}+2}$,
所以抛物线与x轴的两个交点和它的顶点所组成的三角形面积=$\frac{1}{2}$•(m2+4m+6)•2$\sqrt{(m+2)^{2}+2}$=[(m+2)2+2]•$\sqrt{(m+2)^{2}+2}$,
因为m=-2时,(m+2)2+2有最小值2,$\sqrt{(m+2)^{2}+2}$也有最小值$\sqrt{2}$,
所以抛物线与x轴的两个交点和它的顶点所组成的三角形面积的最小值为2$\sqrt{2}$.
故答案为:-2,2$\sqrt{2}$.
点评 本题考查了抛物线与x轴的交点,二次函数的性质,三角形的面积的计算,求最小值问题,能确定代数式的最小值是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,已知点A是⊙O上一点,直线MN过点A,点B是MN上的另一点,点C是OB的中点,AC=$\frac{1}{2}$OB,若点P是⊙O上的一个动点,且∠OBA=30°,AB=$2\sqrt{3}$时,求△APC的面积的最大值.
如图,已知点A是⊙O上一点,直线MN过点A,点B是MN上的另一点,点C是OB的中点,AC=$\frac{1}{2}$OB,若点P是⊙O上的一个动点,且∠OBA=30°,AB=$2\sqrt{3}$时,求△APC的面积的最大值.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
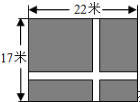 如图,在一块长为22m,宽为17m的矩形地面内,要修筑两条同样宽且互相垂直的道路(两条道路分别与矩形的一条边平行),余下的铺上草坪,要使草坪的面积达到300m2.设道路的宽为x m,根据题意列方程(20-x)(32-x)=300.
如图,在一块长为22m,宽为17m的矩形地面内,要修筑两条同样宽且互相垂直的道路(两条道路分别与矩形的一条边平行),余下的铺上草坪,要使草坪的面积达到300m2.设道路的宽为x m,根据题意列方程(20-x)(32-x)=300.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
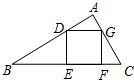 如图,△ABC中∠BAC=90°,正方形DEFG内接于△ABC,且△BDE、△CFG的面积分别为4、1,则△ADG的面积是$\frac{4}{5}$.
如图,△ABC中∠BAC=90°,正方形DEFG内接于△ABC,且△BDE、△CFG的面积分别为4、1,则△ADG的面积是$\frac{4}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>1 | B. | k>$\frac{1}{3}$ | C. | $\frac{1}{3}$<k<1 | D. | k<$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com