
 某家庭装修房屋,由甲乙两个装修公司合作完成先由甲装修公司单独装修3天,剩下的工作由甲乙两个公司合作完成.工程进度满足如图所示的函数关系(x为天数,y为工作量),该家庭共支付工资8000元,若按完成工作量的多少支付工资,装修完后甲装修公司应得多少元?
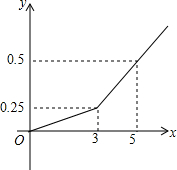
某家庭装修房屋,由甲乙两个装修公司合作完成先由甲装修公司单独装修3天,剩下的工作由甲乙两个公司合作完成.工程进度满足如图所示的函数关系(x为天数,y为工作量),该家庭共支付工资8000元,若按完成工作量的多少支付工资,装修完后甲装修公司应得多少元? 分析 先利用待定系数法求出合作部分一次函数的表达式为y=$\frac{1}{8}$x-$\frac{1}{8}$,再将y=1代入,求出x=9,即完成此房屋装修共需9天.由正比例函数图象可知甲的工作效率为$\frac{1}{12}$,共作了9天,那么其工作量为$\frac{1}{12}$×9=$\frac{3}{4}$,再乘以总价钱8000,就可算出应得工资.
解答 解:设合作部分一次函数的解析式是y=kx+b(k≠0,k,b是常数),
∵图象经过(3,0.25)和(5,0.5),
∴$\left\{\begin{array}{l}{3k+b=0.25}\\{5k+b=0.5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{8}}\\{b=-\frac{1}{8}}\end{array}\right.$,
∴合作部分一次函数的表达式为y=$\frac{1}{8}$x-$\frac{1}{8}$,
∴当y=1时,$\frac{1}{8}$x-$\frac{1}{8}$=1,解得x=9,
即完成此房屋装修共需9天.
由正比例函数图象可知:甲的工作效率是0.25÷3=$\frac{1}{12}$,甲9天完成的工作量是:$\frac{1}{12}$×9=$\frac{3}{4}$,
所以甲得到的工资是:$\frac{3}{4}$×8000=6000(元).
点评 此题考查了一次函数的应用,关键运用了工作效率=工作总量÷工作时间.解决问题的关键是求出甲的工作时间与工作效率.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在Rt△ABC中,∠C=90°.
在Rt△ABC中,∠C=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
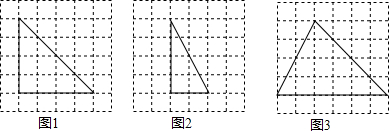
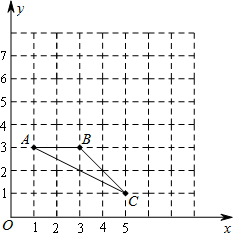 已知△ABC在平面直角坐标系中的位置如图所示.画出△ABC绕点A逆时针旋转90°后的△AB′C′,并写出点B,C的对应点B′,C′的坐标.
已知△ABC在平面直角坐标系中的位置如图所示.画出△ABC绕点A逆时针旋转90°后的△AB′C′,并写出点B,C的对应点B′,C′的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com