
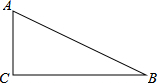
 在Rt△ABC中,∠C=90°.
在Rt△ABC中,∠C=90°.分析 (1)首先以A为圆心,任意长为半径画弧,两弧交AB、AC于N、M两点;再分别以M、N为圆心,大于$\frac{1}{2}$MN长为半径画弧,两弧交于一点O,画射线BO交AC于D即可;
(2)根据垂直平分线的性质,得到BD=AD,进而得到∠ABD=∠DAB,设∠B=x°,根据直角三角形中两个锐角互余可得关于x的方程,解方程即可.
解答 解:(1)如图所示: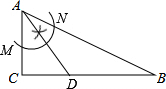
(2)∵AD是∠BAC的平分线,
∴∠CAD=∠BAD,
∵D在线段AB的垂直平分线上,
∴BD=AD,
∴∠ABD=∠DAB,
设∠B=x°,
则∠ABD=∠DAB=∠B=x°,
∵∠C=90°,
∴∠B+∠CAB=90°,
即3x=90°,
解得x=30°,
∴∠BAC=90°-30°=60°.
点评 此题主要考查了作一个角的角平分线,线段的垂直平分线的性质,直角三角形的两锐角互余,掌握基本性质是解决问题的关键.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠ACB=90°,AC=BC=9cm,动点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设Q点运动的时间为t秒,若四边形QP′CP为菱形,则t的值为3.
如图,在Rt△ABC中,∠ACB=90°,AC=BC=9cm,动点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设Q点运动的时间为t秒,若四边形QP′CP为菱形,则t的值为3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
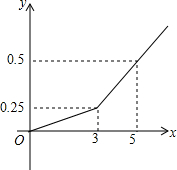 某家庭装修房屋,由甲乙两个装修公司合作完成先由甲装修公司单独装修3天,剩下的工作由甲乙两个公司合作完成.工程进度满足如图所示的函数关系(x为天数,y为工作量),该家庭共支付工资8000元,若按完成工作量的多少支付工资,装修完后甲装修公司应得多少元?
某家庭装修房屋,由甲乙两个装修公司合作完成先由甲装修公司单独装修3天,剩下的工作由甲乙两个公司合作完成.工程进度满足如图所示的函数关系(x为天数,y为工作量),该家庭共支付工资8000元,若按完成工作量的多少支付工资,装修完后甲装修公司应得多少元?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
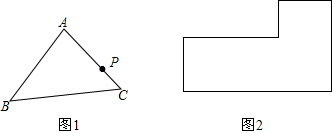
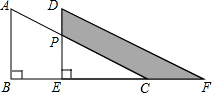 如图是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移得到△DEF.若AB=8,BE=6,DP=4,则图中阴影部分的面积为36cm2.
如图是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移得到△DEF.若AB=8,BE=6,DP=4,则图中阴影部分的面积为36cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com