
 x和y=-x+m,二次函数y=x2+px+q的图象的顶点为M.
x和y=-x+m,二次函数y=x2+px+q的图象的顶点为M. x与y=-x+m的交点处,试证明:无论m取何实数值,二次函数y=x2+px+q的图象与直线y=-x+m总有两个不同的交点.
x与y=-x+m的交点处,试证明:无论m取何实数值,二次函数y=x2+px+q的图象与直线y=-x+m总有两个不同的交点. 直线y=
直线y= x上求异于M的点P,使点P在△CMA的外接圆上.
x上求异于M的点P,使点P在△CMA的外接圆上.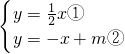 有
有 =-x+m
=-x+m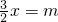 ,
,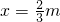 ,
,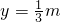 ,
, ,
,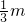 ),
), m)2+
m)2+ m=
m=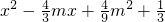 m③
m③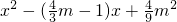
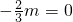
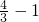 )2]-4(
)2]-4(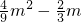 )
)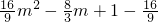 m2+
m2+
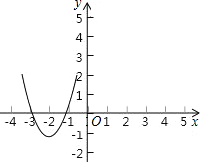
 x上,可设P(n,
x上,可设P(n, n),
n),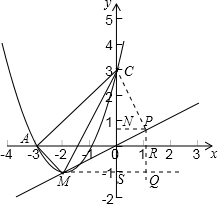
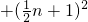
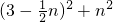 ,
,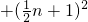 +
+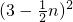 +n2=20,
+n2=20,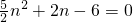 ,
, ,n2=-2,
,n2=-2, ,此时
,此时 ,
, ,
, ).
). x和y=-x+m相交,解出交点,二次函数y=x2+px+q的图象的顶点为M,M是交点,写出二次函数带有m的函数关系式,再解出根的判别式,可证交点的个数.
x和y=-x+m相交,解出交点,二次函数y=x2+px+q的图象的顶点为M,M是交点,写出二次函数带有m的函数关系式,再解出根的判别式,可证交点的个数. n),分别作PN⊥y轴于N,PQ⊥x轴于R,过M作MS⊥y轴于S,MS的延长线与PR的延长线交于点Q.由勾股定理|MP|2=|MQ|2+|QP|2,然后解出n.
n),分别作PN⊥y轴于N,PQ⊥x轴于R,过M作MS⊥y轴于S,MS的延长线与PR的延长线交于点Q.由勾股定理|MP|2=|MQ|2+|QP|2,然后解出n.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
 直线y=
直线y=| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
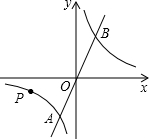 如图,已知直线y=2x和双曲线y=
如图,已知直线y=2x和双曲线y=| 2 | x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com