考点:反比例函数图象上点的坐标特征,坐标与图形变化-平移
专题:计算题,压轴题
分析:设P点坐标为(a,b)过A点、B点分别作AC⊥y轴,BD⊥y轴,如图,则OA=
OC=
AC,BD=2OD,OB=
OD,则得到点P沿射线OA的方向平移2
个单位时,相当于向下平移2个单位,向右平移了2个单位,所以P
1的坐标为(a+2,b-2);同理得到P
2的坐标为(a+6,b-3);然后根据反比例函数图象上点的坐标特征得
| | (a+2)(b-2)=ab | | (a+6)(b-3)=ab |
| |
,解得a与b的值,于是k=ab=8.
解答:解:设P点坐标为(a,b),
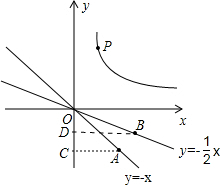
过A点、B点分别作AC⊥y轴,BD⊥y轴,如图,则OA=
OC=
AC,BD=2OD,OB=
OD,
当点P沿射线OA的方向平移2
个单位时,相当于向下平移2个单位,向右平移了2个单位,所以P
1的坐标为(a+2,b-2);
当点P沿沿射线OB的方向平移3
个单位时,相当于向下平移3个单位,向右平移了6个单位,所以P
2的坐标为(a+6,b-3);
因为点P、P
1和P
2都在图象y=
上,
所以
| | (a+2)(b-2)=ab | | (a+6)(b-3)=ab |
| |
,
解得
,
所以k=ab=8.
故答案为8.
点评:本题考查了反比例函数图象上点的坐标特征:反比例函数y=
(k≠0)图象上点的横纵坐标之积为k.也考查了坐标与图象变化-平移.

 如图,在平面直角坐标系中,第一象限内的双曲线y=
如图,在平面直角坐标系中,第一象限内的双曲线y=


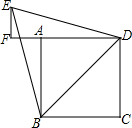 已知四边形ABCD是边长为2的正方形,以对角线BD为边作正三角形BDE,过E作DA的延长线的垂线EF,垂足为F.
已知四边形ABCD是边长为2的正方形,以对角线BD为边作正三角形BDE,过E作DA的延长线的垂线EF,垂足为F. 2014年巴西世界杯特许商品零售店新进一批吉祥物Fuleco(三色犰狳),每个进价150元,售价为200元,每天可以卖20个,为打开市场,商家决定降价销售,市场调研员根据调查,整理出售价(150元-200之间)与每天销售量的相关信息如下:
2014年巴西世界杯特许商品零售店新进一批吉祥物Fuleco(三色犰狳),每个进价150元,售价为200元,每天可以卖20个,为打开市场,商家决定降价销售,市场调研员根据调查,整理出售价(150元-200之间)与每天销售量的相关信息如下: