
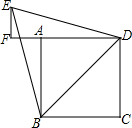
 已知四边形ABCD是边长为2的正方形,以对角线BD为边作正三角形BDE,过E作DA的延长线的垂线EF,垂足为F.
已知四边形ABCD是边长为2的正方形,以对角线BD为边作正三角形BDE,过E作DA的延长线的垂线EF,垂足为F.| 2 |
| 2 |
| 2 |
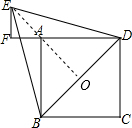 连接EA,且延长交BD于O,
连接EA,且延长交BD于O,| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 3 |
| 3 |
| 3 |


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
 如图,已知△ABC和点P.
如图,已知△ABC和点P.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,矩形ABCD中,AB=6,AD=8,顺次连结各边中点得到四边形A1B1C1D1,再顺次连结四边形A1B1C1D1各边中点得到四边形A2B2C2D2…,依此类推,则四边形A7B7C7D7的周长为( )
如图,矩形ABCD中,AB=6,AD=8,顺次连结各边中点得到四边形A1B1C1D1,再顺次连结四边形A1B1C1D1各边中点得到四边形A2B2C2D2…,依此类推,则四边形A7B7C7D7的周长为( )| A、14 | B、10 | C、5 | D、2.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,第一象限内的双曲线y=
如图,在平面直角坐标系中,第一象限内的双曲线y=| k |
| x |
| 2 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源: 题型:
| A、了解全市中学生的心理健康状况 |
| B、了解某班同学“立定跳远”的成绩 |
| C、了解重庆市的空气质量情况 |
| D、了解端午节期间重庆市场上的粽子质量情况 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com