
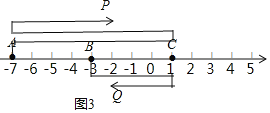
����Ŀ����֪�������ϵ�A��C��Ӧ�����ֱ�Ϊa��c��������|a+7|+��c��1��2020��0����B��Ӧ����Ϊ��3��

��1��������ͼ��ʾ�������ϱ�ʾ����A��C��Ӧ��λ�ã�
��2��������P��Q�ֱ��A��Bͬʱ���������˶�����P���ٶ�Ϊ3����λ�����룻��Q���ٶ�Ϊ1����λ�����룬��Q�˶�����C����ԭ�ٷ��أ������B��ֹͣ�˶�����P�˶�����C������ԭ�ٷ��أ������A�����۷���C�˶�������Qֹͣ�˶�ʱ��P��ֹ֮ͣ�˶������ڱ���ͼ�л��������˶�����������P��Qͬʱ����������ij��Ĵ���ʾ��ͼ��������õ��������ϱ�ʾ������
���𰸡���1����A��ʾ����Ϊ��7��C���ʾ����Ϊ1����2���������˶�����������P��Qͬʱ����������ij���ʾ����Ϊ��2��0��1��
��������
��1�����÷Ǹ������������a��c��Ȼ���������ϱ�ʾ������
��2����P��Q���˶���ʱ��Ϊt��s��ʱ������AB=4��CB=4��AC=8����P���A����C���˶���Q���B����C���˶�ʱ����ͼ1�������������з���3t-t=4����P���A���˶���C�㣬�۷����ٴ�C����A���˶���Q���B����C���˶�����ͼ2��������������õ�3t-8+t=4����P���A�㵽��C���۷����ٴ�C���˶���A�㣬�����۷���C���˶���Q���B���˶���C��ʱ���۷�����B���˶�����ͼ3��������������õ�3t-16+t-4=8��Ȼ��ֱ�ⷽ�����t���Ӷ��õ��������ʾ������
�⣺��1����|a+7|+��c��1��2020��0��
��a+7��0��c��1��0��
��a����7��c��1��
����A��ʾ����Ϊ��7��C���ʾ����Ϊ1��
��ͼ��
![]()
��2����P��Q���˶���ʱ��Ϊt��s��ʱ������AB����3������7����4��CB��1������3����4��AC��8��
��P���A����C���˶���Q���B����C���˶�ʱ����ͼ1��
3t��t��4�����t��2��
��ʱ�������ʾ����Ϊ��3+t����3+2����1��
��P���A���˶���C�㣬�۷����ٴ�C����A���˶���Q���B����C���˶�����ͼ2��
3t��8+t��4�����t��3��
��ʱ�������ʾ����Ϊ��3+3t����3+3��0��
��P���A�㵽��C���۷����ٴ�C���˶���A�㣬�����۷���C���˶���Q���B���˶���C��ʱ���۷�����B���˶�����ͼ3��
3t��16+t��4��8�����t��7��
��ʱ�������ʾ����Ϊ��3+4����t��4������2��
���������������˶�����������P��Qͬʱ����������ij���ʾ����Ϊ��2��0��1��



 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() �뷴��������
�뷴��������![]() ��ͼ����
��ͼ����![]() ��
��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����֪��
����֪��![]() ������Ϊ
������Ϊ![]() ��
��
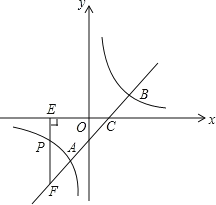
��1�����������Ľ���ʽ��
��2������![]() �Ƿ���������ͼ����һ�㣬����
�Ƿ���������ͼ����һ�㣬����![]() ��
��![]() ���ڵ�
���ڵ�![]() ���ӳ�
���ӳ�![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() ����
����![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
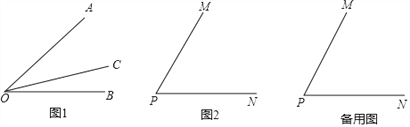
����Ŀ����̽����֪������ͼ1������OC�ڡ�AOB���ڲ���ͼ�й���3���ǣ���AOB����AOC�͡�BOC����������һ���ǵĶ�������һ���Ƕ������������������OC�ǡ�AOB�����ɷ�������
��1��һ���ǵ�ƽ������ ������ǵ����ɷ�����������������������������
��2����ͼ2������MPN=����������PQ�ǡ�MPN�����ɷ����������MPQ=�� �������ú����Ĵ���ʽ��ʾ�����п��ܵĽ����
�������о�������ͼ2������MPN=60����������PQ�Ƶ�P��PNλ�ÿ�ʼ����ÿ��10�����ٶ���ʱ����ת����PQ��PN��180��ʱֹͣ��ת����ת��ʱ��Ϊt�룮
��3����tΪ��ֵʱ������PM�ǡ�QPN�����ɷ�������
��4��������PMͬʱ�Ƶ�P��ÿ��5�����ٶ���ʱ����ת������PQͬʱֹͣ����ֱ��д��������PQ�ǡ�MPN�����ɷ�����ʱt��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����M��Բһ����Χ�������丨���źţ�һ���ִ��ں��ϴ���������һ�����ٶ����ٺ��У��ִ���A����õ���M�ڱ�ƫ��30��������ʻ1Сʱ��B������ʱ�պý������M�������ź�������õ���M�ڱ�ƫ��45���������ִ�ͨ������M�������ź�����ʱ��Ϊ��������
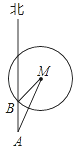
A. ��![]() ��1��Сʱ B. ��
��1��Сʱ B. ��![]() +1��Сʱ C. 2Сʱ D.
+1��Сʱ C. 2Сʱ D. ![]() Сʱ
Сʱ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�AOB�����߽�ȡOA=OB��OC=OD������AD��BC���ڵ�P�������н����Т١�AOD�ա�BOC���ڡ�APC�ա�BPD���۵�P�ڡ�AOB��ƽ�����ϣ���ȷ����__��������ţ�
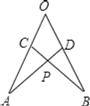
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AD��BC��DC��BC�� AEƽ�֡�BAD, EΪCD�е㣬��̽��AD��BC��AB֮���кι�ϵ����˵�����ɣ�
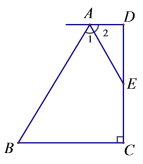
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ�µ�һ������������ʵ��������Ҫ��������ʵ�����Ա����ʦһ�˵���������Ҫ40������ɣ���������ʦ�빤����ʦ����ͬ����20���Ӻ�����ʦ�����������ʦ���ٵ���������20���Ӳ��������
��1����ʦ��������������ʵ��������Ҫ���ٷ��ӣ�
��2��ѧУҪ����ʦ���Ĺ���ʱ�䲻�ܳ���30���ӣ�Ҫ��������������ģ�����ʦ����Ҫ�������ٷ��ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=5��AC=3����BC���ϵ�����AD��ȡֵ��Χ�ǣ� ��.
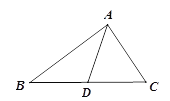
A. 2<AD<8B. 0<AD<8C. 1<AD<4D. 3<AD<5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
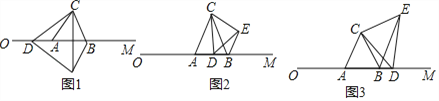
����Ŀ����14�֣���ͼ1����ABC�DZ߳�Ϊ4cm�ĵȱ������Σ���AB������OM�ϣ���OA=6cm����D��O���������OM�ķ�����1cm/s���ٶ��˶�����D�����A�غ�ʱ������ACD�Ƶ�C��ʱ�뷽����ת60��õ���BCE������DE��
��1����֤����CDE�ǵȱ������Σ�
��2����ͼ2����6��t��10ʱ����BDE���ܳ��Ƿ������Сֵ�������ڣ������BDE����С�ܳ����������ڣ���˵�����ɣ�
��3����ͼ3������D������OM���˶�ʱ���Ƿ������D��E��BΪ�������������ֱ�������Σ������ڣ������ʱt��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com