
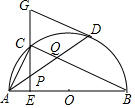
 如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,给出下列结论:①∠DAC=∠ABC;②AD=CB;③点P是△ACQ的外心;④AC2=AE•AB;⑤CB∥GD,其中正确的结论是( )
如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,给出下列结论:①∠DAC=∠ABC;②AD=CB;③点P是△ACQ的外心;④AC2=AE•AB;⑤CB∥GD,其中正确的结论是( )| A. | ①③⑤ | B. | ②④⑤ | C. | ①②⑤ | D. | ①③④ |
分析 在同圆或等圆中,同弧或等弧所对的圆周角相等,据此推理可得①正确,②错误;通过推理可得∠ACE=∠CAP,得出AP=CP,再根据∠PCQ=∠PQC,可得出PC=PQ,进而得到AP=PQ,即P为Rt△ACQ斜边AQ的中点,故P为Rt△ACQ的外心,即可得出③正确;连接BD,则∠ADG=∠ABD,根据∠ADG≠∠BAC,∠BAC=∠BCE=∠PQC,可得出∠ADG≠∠PQC,进而得到CB与GD不平行,可得⑤错误.
解答  解:∵在⊙O中,点C是$\widehat{AD}$的中点,
解:∵在⊙O中,点C是$\widehat{AD}$的中点,
∴$\widehat{AC}$=$\widehat{CD}$,
∴∠CAD=∠ABC,故①正确;
∵$\widehat{AC}$≠$\widehat{BD}$,
∴$\widehat{AD}$≠$\widehat{BC}$,
∴AD≠BC,故②错误;
∵AB是⊙O的直径,
∴∠ACB=90°,
又∵CE⊥AB,
∴∠ACE+∠CAE=∠ABC+∠CAE=90°,
∴∠ACE=∠ABC,
又∵C为$\widehat{AD}$的中点,
∴$\widehat{AC}$=$\widehat{CD}$,
∴∠CAP=∠ABC,
∴∠ACE=∠CAP,
∴AP=CP,
∵∠ACQ=90°,
∴∠ACP+∠PCQ=∠CAP+∠PQC=90°,
∴∠PCQ=∠PQC,
∴PC=PQ,
∴AP=PQ,即P为Rt△ACQ斜边AQ的中点,
∴P为Rt△ACQ的外心,故③正确;
∵AB是⊙O的直径,
∴∠ACB=90°,
又∵CE⊥AB
∴根据射影定理,可得AC2=AE•AB,故④正确;
如图,连接BD,则∠ADG=∠ABD,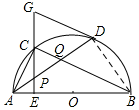
∵$\widehat{AC}$≠$\widehat{BD}$,
∴$\widehat{AD}$≠$\widehat{BC}$,
∴∠ABD≠∠BAC,
∴∠ADG≠∠BAC,
又∵∠BAC=∠BCE=∠PQC,
∴∠ADG≠∠PQC,
∴CB与GD不平行,故⑤错误.
故答案为:D.
点评 此题主要考查了切线的性质,圆周角定理,射影定理,圆心角、弧、弦的关系,相似三角形的判定与性质以及三角形的外接圆与圆心的综合应用,熟练掌握性质及定理是解决本题的关键.解题时注意:弦切角等于弦所对的圆周角.


科目:初中数学 来源: 题型:选择题
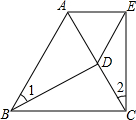 如图,D是等边三角形ABC的边AC上一点,E是等边三角形ABC外一点,若BD=CE,∠1=∠2,则△ADE的形状是( )
如图,D是等边三角形ABC的边AC上一点,E是等边三角形ABC外一点,若BD=CE,∠1=∠2,则△ADE的形状是( )| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 不等边三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在反比例函数y=$\frac{4}{x}$(x>0)的图象上,有点P1,P2,P3,P4…Pn(n为正整数,且n≥1).它们的横坐标依次为1,2,3,4…n(n为正整数,且n≥1),分别过这些点作x轴与y轴的垂线,连接相邻两点,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3…Sn-1(n为正整数,且n≥2),那么S2+S3+S4+…S7=$\frac{3}{4}$.
如图,在反比例函数y=$\frac{4}{x}$(x>0)的图象上,有点P1,P2,P3,P4…Pn(n为正整数,且n≥1).它们的横坐标依次为1,2,3,4…n(n为正整数,且n≥1),分别过这些点作x轴与y轴的垂线,连接相邻两点,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3…Sn-1(n为正整数,且n≥2),那么S2+S3+S4+…S7=$\frac{3}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
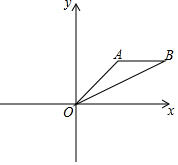 如图,△ABO中,点O是坐标原点,A(2,2),B(4,2),点C在x轴正半轴上,O,B,C三点所构成的三角形与△ABO相似,则点C的坐标是(2,0)或(10,0).
如图,△ABO中,点O是坐标原点,A(2,2),B(4,2),点C在x轴正半轴上,O,B,C三点所构成的三角形与△ABO相似,则点C的坐标是(2,0)或(10,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
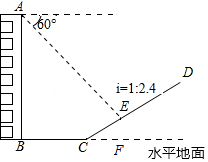 如图,一楼房AB后有一小山坡,其坡度为i=1:2.4,山坡坡面上E点处有一亭子,测得山坡脚C与楼房水平距离BC=30米,与亭子距离CE=26米,小丽从楼房顶测得E点的俯角为60°,求楼房AB的高.
如图,一楼房AB后有一小山坡,其坡度为i=1:2.4,山坡坡面上E点处有一亭子,测得山坡脚C与楼房水平距离BC=30米,与亭子距离CE=26米,小丽从楼房顶测得E点的俯角为60°,求楼房AB的高.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com