
【题目】如图,在平面直角坐标系xOy中,函数![]() 的图象
的图象![]() 是第二、四象限的角平分线.
是第二、四象限的角平分线.

(1)实验与探究:由图观察易知A(-1,3)关于直线![]() 的对称点
的对称点![]() 的坐标为(-3,1),请你写出点B(5,3)关于直线
的坐标为(-3,1),请你写出点B(5,3)关于直线![]() 的对称点
的对称点![]() 的坐标为 ;
的坐标为 ;
(2)归纳与发现:结合图形,自己选点再试一试,通过观察点的坐标,你会发现:坐标平面内任一点P(m ,n)关于第二、四象限的角平分线![]() 的对称点
的对称点![]() 的坐标为 ;
的坐标为 ;
(3)运用与拓广:已知两点C(6 , 0),D(2 , 4),试在直线![]() 上确定一点,使这点到C,D两点的距离之和最小,在图中画出这点的位置,保留作图痕迹,并求出这点的坐标.
上确定一点,使这点到C,D两点的距离之和最小,在图中画出这点的位置,保留作图痕迹,并求出这点的坐标.
【答案】(1)![]() (-3,-5).(2)
(-3,-5).(2)![]() (-n,-m).(3)作图参见解析,E(1 ,-1).
(-n,-m).(3)作图参见解析,E(1 ,-1).
【解析】试题分析:(1)由观察得知,关于直线![]() 的对称点的坐标,横纵坐标颠倒,且是原数的相反数即B′(-3,-5);(2)通过选点验证,坐标平面内任一点P(m ,n)关于第二、四象限的角平分线
的对称点的坐标,横纵坐标颠倒,且是原数的相反数即B′(-3,-5);(2)通过选点验证,坐标平面内任一点P(m ,n)关于第二、四象限的角平分线![]() 的对称点
的对称点![]() 的坐标为(-n,-m);(3)先描点,在坐标平面内找到C,D两点,然后在直线
的坐标为(-n,-m);(3)先描点,在坐标平面内找到C,D两点,然后在直线![]() 上确定一点E,,使这点到C,D两点的距离之和最小,作点C关于直线 L的对称点
上确定一点E,,使这点到C,D两点的距离之和最小,作点C关于直线 L的对称点![]() ,连接
,连接![]() D,交 L于点E,由线段垂直平分线性质和两点之间线段最短可知E点即为所求,根据前面的规律把C′点坐标写出来,再把DC′的解析式求出来,和直线y=-x组成方程组求解,
D,交 L于点E,由线段垂直平分线性质和两点之间线段最短可知E点即为所求,根据前面的规律把C′点坐标写出来,再把DC′的解析式求出来,和直线y=-x组成方程组求解,
试题解析:(1)由观察得知,关于直线![]() 的对称点的坐标,横纵坐标颠倒,且是原数的相反数,B(5,3)颠倒后是(3,5),再是原数的相反数是(-3,-5),∴
的对称点的坐标,横纵坐标颠倒,且是原数的相反数,B(5,3)颠倒后是(3,5),再是原数的相反数是(-3,-5),∴![]() (-3,-5).(2)通过选点验证,坐标平面内任一点P(m ,n)关于第二、四象限的角平分线
(-3,-5).(2)通过选点验证,坐标平面内任一点P(m ,n)关于第二、四象限的角平分线![]() 的对称点为
的对称点为![]() (-n,-m);(3)如图,作点C关于直线 L的对称点
(-n,-m);(3)如图,作点C关于直线 L的对称点![]() ,连接
,连接![]() D,交 L于点E,连接CE.由作图可知,EC= E
D,交 L于点E,连接CE.由作图可知,EC= E![]() ,∴EC + ED = E
,∴EC + ED = E![]() + ED =
+ ED =![]() D .因为两点之间线段最短,∴点E为所求.∵C(6,0),∴
D .因为两点之间线段最短,∴点E为所求.∵C(6,0),∴![]() (0,-6).设直线
(0,-6).设直线![]() D的解析式为
D的解析式为![]() .∵D(2 , 4),∴
.∵D(2 , 4),∴![]() .∴直线
.∴直线![]() D的解析式为
D的解析式为![]() .由
.由![]() 得
得![]() ,∴E(1 , -1).
,∴E(1 , -1).



 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】北京在今年6月初申办2022年冬季奥运会的陈述中,若申办成功,将带动月3.2亿人参与这项活动.将3.2亿用科学记数法表示为( )
A.32×107
B.3.2×108
C.3.2×109
D.0.32×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市账目记录显示,第一天卖出39支牙刷和21盒牙膏,收入300元;第二天以同样的价格卖出同样的52支牙刷和28盒牙膏,收入应该是____________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表为深圳市居民每月用水收费标准,(单位:元/m3).
用水量 | 单价 |
x≤22 | a |
剩余部分 | a+1.1 |
(1)某用户用水10立方米,共交水费23元,求a的值;
(2)在(1)的前提下,该用户5月份交水费71元,请问该用户用水多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
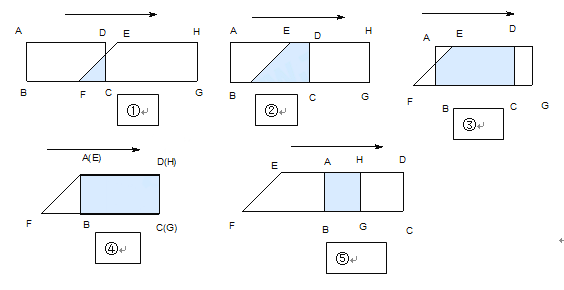
【题目】已知:如图,在矩形ABCD中,AD=6㎝,AB=3㎝。在直角梯形中EFGH中 ,EH∥FG ,∠EFG=![]() ,∠G=
,∠G=![]() ,EH=6㎝,HG=3㎝。B、C、F、G同在一条直线上。当F、C两点重合时,矩形ABCD以1㎝/秒的速度沿直线按箭头所示的方向匀速平移,
,EH=6㎝,HG=3㎝。B、C、F、G同在一条直线上。当F、C两点重合时,矩形ABCD以1㎝/秒的速度沿直线按箭头所示的方向匀速平移, ![]() 秒后,矩形ABCD与梯形EFGH重合部分的面积为
秒后,矩形ABCD与梯形EFGH重合部分的面积为![]() ㎝。按要求回答下列各题(不要求写出解题过程):
㎝。按要求回答下列各题(不要求写出解题过程):
(1)当![]() 时,
时, ![]() cm2(如图①);
cm2(如图①);
当![]() 时,
时, ![]() cm2(如图④);
cm2(如图④);
(2)在下列各种情况下,分别用![]() 表示
表示![]() :
:
如图①,当![]() 时,
时, ![]() cm2;
cm2;
如图②,当![]() 时,
时, ![]() cm2;
cm2;
如图③,当![]() 时,
时, ![]() cm2;
cm2;
如图⑤,当![]() 时,
时, ![]() cm2.
cm2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com