
【题目】计算下列各题:
(1)![]() +(-
+(- ![]() )-(-
)-(- ![]() )+(+
)+(+ ![]() );
);
(2)![]() +(-71) +
+(-71) + ![]() +(-9 );
+(-9 );
(3)-9 ![]() ×81
×81
(4)(﹣36)×(﹣ ![]() +
+ ![]() ﹣
﹣ ![]() )
)
(5)-15+(-2)2×( ![]() -
- ![]() )-
)- ![]() ÷3;
÷3;
(6)![]()
【答案】
(1)解:原式=![]()
=![]()
=![]()
(2)解:原式=45-71+5-9
=(45+5)-(71+9)
=50-80
=-30
(3)解:原式=(10-![]() )×81
)×81
=10×81-![]() ×81
×81
=810-9
=-801
(4)解:原式=(-36)×(-![]() )+(-36)×
)+(-36)×![]() +(-36)×(-
+(-36)×(-![]() )
)
=16-30+21
=7
(5)解:原式=-1+4×(-![]() )-
)-![]() ×
×![]()
=-1-![]() -
-![]()
=- ![]()
(6)解:原式=-1-![]() ×
×![]() ×(2-9)
×(2-9)
=-1-![]() ×(-7)
×(-7)
=-1+![]()
=![]()
![]()
【解析】(1)根据有理数加减法法则及去括号法则计算即可.
(2)根据有理数加减法法则及去括号法则、绝对值的性质计算即可.
(3)根据有理数乘法运算定律和有理数加减法法则计算即可.
(4)根据有理数乘法运算定律和有理数加减法法则计算即可.
(5)根据有理数乘方及有理数混合运算则计算即可.
(6)根据有理数乘方及有理数混合运算则计算即可.
【考点精析】根据题目的已知条件,利用有理数的加减混合运算和绝对值的相关知识可以得到问题的答案,需要掌握混合运算法则:先乘方,后乘除,最后加减;正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离.


科目:初中数学 来源: 题型:
【题目】我市某蔬菜生产基地在气温较低时,用装有恒温系统的大鹏栽培一种在自然光照且温度为18℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=![]() 的一部分.请根据图中信息解析下列问题:
的一部分.请根据图中信息解析下列问题:
(1)求y与x的函数关系式;
(2)当x=16时,大棚内的温度约为多少度?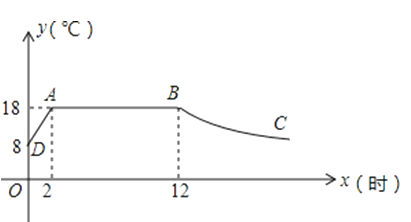
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为5,点P在⊙O外,PB交⊙O于A、B两点,PC交⊙O于D、C两点.
(1)求证:PAPB=PDPC;
(2)若PA=![]() ,AB=
,AB=![]() ,PD=DC+2,求点O到PC的距离.
,PD=DC+2,求点O到PC的距离.
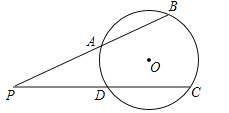
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1):△ABC中,∠B、∠C的平分线相交于点O,过点O作EF∥BC分别交AB、AC于E、F. 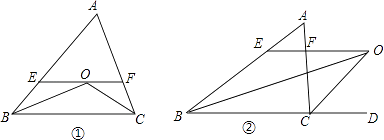
(1)EF与BE、CF之间有什么关系?(不证明)
(2)若△ABC中,∠B的平分线与三角外角∠ACD的平分线CO交于点O,过点O作OE∥BC交AB于E,交AC于F(图示),EF与BE,CF之间又有怎样的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,![]() ,
,![]() .若S=3,则
.若S=3,则![]() 的值为( )
的值为( )
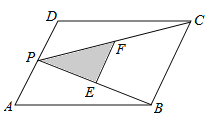
A.24 B.12 C.6 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下图是汽车行驶速度(千米/时)和时间(分)的关系图,下列说法其中正确的个数为( )
( 1 )汽车行驶时间为40分钟;
( 2 )AB表示汽车匀速行驶;
( 3 )在第30分钟时,汽车的速度是90千米/时;
( 4 )第40分钟时,汽车停下来了.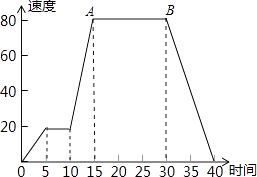
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,∠3=∠4,∠E=90°,试问:AB∥CD吗?为什么?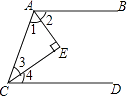
解:∵∠1+∠3+∠E=180°∠E=90°
∴∠1+∠3=
∵∠1=∠2,∠3=∠4
∴∠1+∠2+∠3+∠4=
∴AB∥CD .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com