练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    把抛物线y=﹣x2向左平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为（ ）

    A．y=﹣（x﹣1）2﹣3 B．y=﹣（x+1）2﹣3 C．y=﹣（x﹣1）2+3 D．y=﹣（x+1）2+3

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016届山东潍坊临朐县、昌邑县中考一模数学试卷（解析版） 题型：解答题

    在平面直角坐标系中，已知等腰梯形ABCD的三个顶点A（-2，0），B（6，0），C（4，6），对角线AC与BD相交于点E．

    （1）求E的坐标；

    （2）若M是x轴上一动点，求MC+MD的最小值；

    （3）在y轴正半轴上求点P，使以P、B、C为顶点的三角形为等腰三角形．

    查看答案和解析>>

    科目：初中数学 来源：2016届山东烟台龙口市中考一模数学试卷（解析版） 题型：选择题

    如图，在△ABC中，AB=CB，以AB为直径的⊙O交AC于点D．过点C作CF∥AB，在CF上取一点E，使DE=CD，连接AE．对于下列结论：①AD=DC；②△CBA∽△CDE；③；④AE为⊙O的切线，一定正确的结论全部包含其中的选项是（ ）

    A．①② B．①②③ C．①④ D．①②④

    查看答案和解析>>

    科目：初中数学 来源：2016届浙江宁波南三县初三上期末数学试卷（解析版） 题型：填空题

    为美化校园，学校决定将花园边墙上的矩形门ABCD改为以AC为直径的圆弧形门，如图所示，量得矩形门宽为1m，对角线AC的长为2m，则要打掉墙体的面积为 m2．

    查看答案和解析>>

    科目：初中数学 来源：2016届浙江宁波南三县初三上期末数学试卷（解析版） 题型：选择题

    如图，抛物线y=ax2+bx+c与x轴的负半轴交于点A，B（点A在点B的右边），与y轴的正半轴交于点C，且OA=OC=1，则下列关系中正确的是（ ）

    A．a+b=1 B．b＜2a C．a﹣b=﹣1 D．ac＜0

    查看答案和解析>>

    科目：初中数学 来源：2016届云南昆明石林县鹿阜中学初三下3月考数学试卷（解析版） 题型：解答题

    如图，已知抛物线y=ax2+bx+4与x轴交于A（﹣2，0）、B两点，与y轴交于C点，其对称轴为直线x=1．

    （1）直接写出抛物线的解析式： ；

    （2）把线段AC沿x轴向右平移，设平移后A、C的对应点分别为A′、C′，当C′落在抛物线上时，求A′、C′的坐标；

    （3）除（2）中的点A′、C′外，在x轴和抛物线上是否还分别存在点E、F，使得以A、C、E、F为顶点的四边形为平行四边形？若存在，求出E、F的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2016届云南昆明石林县鹿阜中学初三下3月考数学试卷（解析版） 题型：解答题

    如图，点B、F、C、E在同一直线上，BF=CE，AC=DF，且AC∥DF，求证：AB=DE．

    查看答案和解析>>

    科目：初中数学 来源：2016届山省济南商河县九年级第二次中考模拟考试数学试卷（解析版） 题型：解答题

    如图，直线与抛物线相交于A(，）和B（4，），点P是线段AB上异于A、B的动点，过点P作PC⊥轴于点D，交抛物线于点C．

    （1）求抛物线的解析式；

    （2）是否存在这样的P点，使线段PC的长有最大值？若存在，求出这个最大值；若不存在，请说明理由；

    （3）求△PAC为直角三角形时点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源：2016届山东聊城阳谷县九年级第一次模拟检测数学试卷（解析版） 题型：选择题

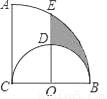
    如图，AC⊥BC，AC=BC=4，以BC为直径作半圆，圆心为点O；以点C为圆心，BC为半径作，过点O作AC的平行线交两弧于点D、E，则阴影部分的面积是（ ）

    A． B． C． D．

    查看答案和解析>>

    同步练习册答案