解:(1)∵四边形ABCD是菱形,
∴AB=BC=CD=DA=2

.
∴AB的中点坐标为(-

,0),CD的中点坐标为(0,3),
分别代入y=ax
2+b,得
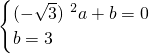
,
解得:

,
∴这条抛物线的函数的解析式为y=-x
2+3;
(2)存在.
如图2所示,在△BCE中,∠BEC=90°,BE=3,BC=2

Sin∠C=

=

=

∠C=60°,∠CBE=30°
∴EC=

BC=

,DE=

又AD∥BC,∴∠ADC+∠C=180°
∴∠ADC=180°-60°=120°
要使△ADC与△DEF相似,则△ADF中必有一个角为直角.
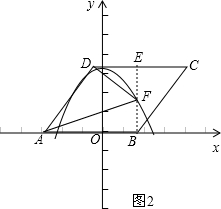
①若∠ADF=90°,∠EDF=120°-90°=30°,在△DEF中,DE=

,得EF=1,DF=2.
又E(t,3),F(t,-t
2+3),
∴EF=3-(-t
2+3)=t
2∴t
2=1∵t>0,∴t=1,
此时,

=
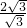
=2,

=

=2,

=

又∵∠ADF=∠DEF∴△ADC∽△DEF.
②若∠DFA=90°,可证得△DEF∽△FBA,则
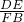
=
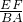
,
设EF=m,则FB=3-m,
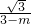
=
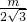
即m
2-3m+6=0,此方程无实数根,此时t不存在;
③由题意得,∠DAF<∠DAB=60°,∴∠DAF≠90°
∴此时t不存在.
综上所述,存在t=1,使△ADC与△DEF相似.
分析:(1)根据已知条件求出AB和CD的中点坐标,然后利用待定系数法求该二次函数的解析式;
(2)①如图2所示,△ADF与△DEF相似,包括三种情况,需要分类讨论:
(I)若∠ADF=90°时,△ADF∽△DEF,求此时t的值;
(II)若∠DFA=90°时,△DEF∽△FBA,利用相似三角形的对应边成比例可以求得相应的t的值;
(III)∠DAF≠90°,此时t不存在;
点评:本题是动线型中考压轴题,考查了二次函数的图象与性质的运用、待定系数法的运用、菱形的性质的运用、相似三角形的判定与性质等重要知识,难度较大,对考生能力要求很高.本题难点在于第(2)问中,需要结合△ADF与△DEF相似的三种情况,分别进行讨论,避免漏解.

 ,点A在x轴的负半轴上,点B在坐标原点,点D的坐标为(-
,点A在x轴的负半轴上,点B在坐标原点,点D的坐标为(- ,3),抛物线y=ax2+b.(a≠0)经过AB、CD两边的中点.
,3),抛物线y=ax2+b.(a≠0)经过AB、CD两边的中点.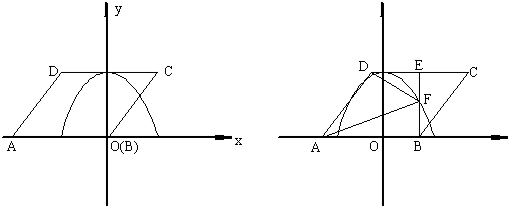
 .
. ,0),CD的中点坐标为(0,3),
,0),CD的中点坐标为(0,3),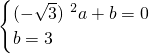 ,
, ,
,
 =
= =
=
 BC=
BC= ,DE=
,DE=

 ,得EF=1,DF=2.
,得EF=1,DF=2. =
=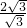 =2,
=2, =
= =2,
=2, =
=
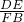 =
=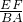 ,
,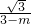 =
=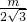 即m2-3m+6=0,此方程无实数根,此时t不存在;
即m2-3m+6=0,此方程无实数根,此时t不存在;


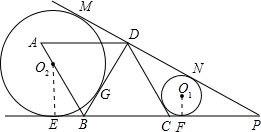 上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G.
上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G.