练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】每年四月北京很多地方杨絮、柳絮如雪花般漫天飞舞，人们不堪其扰。据测定，杨絮纤维的直径约为0.000 010 5米，将0.000 010 5用科学记数法可表示为（ ）
    A.1.05×105
    B.1.05×10-5
    C.0.105×10-4
    D.10.5×10-6

    【答案】B
    【解析】解：绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n ， 与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定，所以0.000 010 5= 1.05×10-5 ，故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，AB∥CD，AB=CD，点E、F在BC上，且BF=CE．

    （1）求证：△ABE≌△DCF；

    （2）试证明：以A、F、D、E为顶点的四边形是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在长方形ABCD中，AB=10厘米，BC=6厘米，点P沿AB边从点A开始向点B以3厘米/秒的速度移动；点Q沿DA边从点D开始向点A以2厘米/秒的速度移动.如果P、Q同时出发，用t (秒）表示移动的时间，那么：

    （1）如图1,用含t的代数式表示AP= ，AQ= .并求出当t为何值时线段AP=AQ.

    （2）如图2,在不考虑点P的情况下，连接QB，问：当t为何值时△QAB的面积等于长方形面积的.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB=AC，∠A=30°，AB的垂直平分线MN交AC于点D，求∠DBC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】AB∥CD，OE平分∠BOC，OF⊥OE，OP⊥CD，∠ABO=a°．则下列结论： ①∠BOE=（180﹣a）°；②OF平分∠BOD；③∠POE=∠BOF；④∠POB=2∠DOF．其中正确结论__________（填编号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面关于三角形内外角平分线所夹角的探究片段，完成所提出的问题．
    探究一：如图1，在△ABC中，已知O是∠ABC与∠ACB的平分线BO和CO的交点，通过分析发现∠BOC=90°+ ∠A，理由如下：
    ∵BO和CO分别是∠ABC与∠ACB的平分线，
    ∴∠1= ∠ABC，∠2= ∠ACB；
    ∴∠1+∠2= （∠ABC+∠ACB）= （180°﹣∠A）=90°﹣ ∠A，
    ∴∠BOC=180°﹣（∠1+∠2）=180°﹣（90°﹣ ∠A）=90°+ ∠A．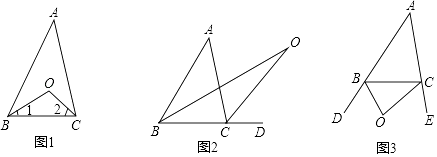

    （1）探究二：如图2中，已知O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？并说明理由．
    （2）探究二：如图3中，已知O是外角∠DBC与外角∠ECB的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，点B、E分别在AC、DF上，BD、CE均与AF相交，∠1=∠2，∠C=∠D，求证：∠A=∠F．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，抛物线y＝﹣（x﹣1）2+2的顶点坐标是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】买一个足球需要m元，买一个篮球需要n元，则买4个足球、7个篮球共需（　　）

    A．28mn 元 B．11mn元 C．（7m+4n）元 D．（4m+7n）元

    查看答案和解析>>

    同步练习册答案