
【题目】阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
探究一:如图1,在△ABC中,已知O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+ ![]() ∠A,理由如下:
∠A,理由如下:
∵BO和CO分别是∠ABC与∠ACB的平分线,
∴∠1= ![]() ∠ABC,∠2=
∠ABC,∠2= ![]() ∠ACB;
∠ACB;
∴∠1+∠2= ![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() (180°﹣∠A)=90°﹣
(180°﹣∠A)=90°﹣ ![]() ∠A,
∠A,
∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣ ![]() ∠A)=90°+
∠A)=90°+ ![]() ∠A.
∠A.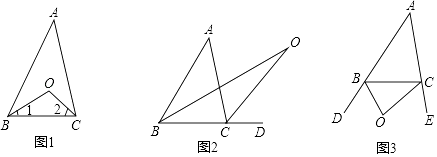
(1)探究二:如图2中,已知O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?并说明理由.
(2)探究二:如图3中,已知O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?
【答案】
(1)解:探究2结论:∠BOC= ![]() ∠A.
∠A.
理由如下:∵BO和CO分别是∠ABC和∠ACD的角平分线,
∴∠1= ![]() ∠ABC,∠2=
∠ABC,∠2= ![]() ∠ACD,
∠ACD,
又∵∠ACD是△ABC的一个外角,
∴∠2= ![]() ∠ACD=
∠ACD= ![]() (∠A+∠ABC)=
(∠A+∠ABC)= ![]() ∠A+∠1,
∠A+∠1,
∵∠2是△BOC的一个外角,
∴∠BOC=∠2﹣∠1= ![]() ∠A+∠1﹣∠1=
∠A+∠1﹣∠1= ![]() ∠A,
∠A,
即∠BOC= ![]() ∠A
∠A
(2)解:由三角形的外角性质和角平分线的定义,∠OBC= ![]() (∠A+∠ACB),∠OCB=
(∠A+∠ACB),∠OCB= ![]() (∠A+∠ABC),
(∠A+∠ABC),
在△BOC中,∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣ ![]() (∠A+∠ACB)﹣
(∠A+∠ACB)﹣ ![]() (∠A+∠ABC),
(∠A+∠ABC),
=180°﹣ ![]() (∠A+∠ACB+∠A+∠ABC),
(∠A+∠ACB+∠A+∠ABC),
=180°﹣ ![]() (180°+∠A),
(180°+∠A),
=90°﹣ ![]() ∠A
∠A
【解析】(1)根据角平分线的定义可得∠1= ![]() ∠ABC,∠2=
∠ABC,∠2= ![]() ∠ACD,再根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义可得∠2=
∠ACD,再根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义可得∠2= ![]() ∠ACD=
∠ACD= ![]() (∠A+∠ABC),∠BOC=∠2﹣∠1,然后整理即可得解;(2)根据三角形的外角性质以及角平分线的定义表示出∠OBC和∠OCB,再根据三角形的内角和定理解答.
(∠A+∠ABC),∠BOC=∠2﹣∠1,然后整理即可得解;(2)根据三角形的外角性质以及角平分线的定义表示出∠OBC和∠OCB,再根据三角形的内角和定理解答.
【考点精析】本题主要考查了三角形的内角和外角和三角形的外角的相关知识点,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
【题目】为了倡导节能低碳的生活,某公司对集体宿舍用电收费作如下规定:一间宿舍一个月用电量不超过a千瓦时,则一个月的电费为20元;若超过a千瓦时,则除了交20元外,超过部分每千瓦时要交![]() 元。某宿舍3月份用电80千瓦时,交电费35元;4月份用电45千瓦时,交电费20元。
元。某宿舍3月份用电80千瓦时,交电费35元;4月份用电45千瓦时,交电费20元。
(1)求a的值;
(2)若该宿舍5月份交电费45元,那么该宿舍当月用电量为多少千瓦时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽妈妈在网上做淘宝生意,专门销售女式鞋子,一次,小丽发现一个进货单上的一个信息是:A款鞋的进价比B款鞋进价多20元,花500元进A款鞋的数量和花400元进B款鞋的数量相同.
(1)问A、B款鞋的进价分别是多少元?
(2)小丽在销售单上记录了两天的数据如表:
日期 | A款女鞋销量 | B款女鞋销量 | 销售总额 |
6月1日 | 12双 | 8双 | 2240元 |
6月2日 | 8双 | 10双 | 1960元 |
请问两种鞋的销售价分别是多少?
(3)小丽妈妈说:“两款鞋的利润率相同”,请通过计算,结合(1)(2)所给信息,判断小丽妈妈的说法是否正确,如果正确,请说明理由;如果错误,能否只调整其中一款的售价,使得两款鞋的利润率相同?能否同时调整两款的售价,使得两款鞋的利润率相同?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年四月北京很多地方杨絮、柳絮如雪花般漫天飞舞,人们不堪其扰。据测定,杨絮纤维的直径约为0.000 010 5米,将0.000 010 5用科学记数法可表示为( )
A.1.05×105
B.1.05×10-5
C.0.105×10-4
D.10.5×10-6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E,F. 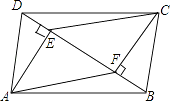
(1)求证:△ADE≌△CBF;
(2)若AC与BD相交于点O,求证:AO=CO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为△ABD的中线. 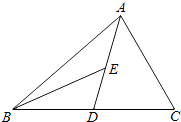
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com