
【题目】四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E,F. 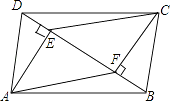
(1)求证:△ADE≌△CBF;
(2)若AC与BD相交于点O,求证:AO=CO.
【答案】
(1)证明:∵BE=DF,
∴BE﹣EF=DF﹣EF,
即BF=DE,
∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB=90°,
在Rt△ADE与Rt△CBF中, ![]() ,
,
∴Rt△ADE≌Rt△CBF
(2)证明:如图,连接AC交BD于O,
∵Rt△ADE≌Rt△CBF,
∴∠ADE=∠CBF,
∴AD∥BC,
∴四边形ABCD是平行四边形,
∴AO=CO.

【解析】(1)根据已知条件得到BF=DE,由垂直的定义得到∠AED=∠CFB=90°,根据全等三角形的判定定理即可得到结论;(2)如图,连接AC交BD于O,根据全等三角形的性质得到∠ADE=∠CBF,由平行线的判定得到AD∥BC,根据平行四边形的性质即可得到结论.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
探究一:如图1,在△ABC中,已知O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+ ![]() ∠A,理由如下:
∠A,理由如下:
∵BO和CO分别是∠ABC与∠ACB的平分线,
∴∠1= ![]() ∠ABC,∠2=
∠ABC,∠2= ![]() ∠ACB;
∠ACB;
∴∠1+∠2= ![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() (180°﹣∠A)=90°﹣
(180°﹣∠A)=90°﹣ ![]() ∠A,
∠A,
∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣ ![]() ∠A)=90°+
∠A)=90°+ ![]() ∠A.
∠A.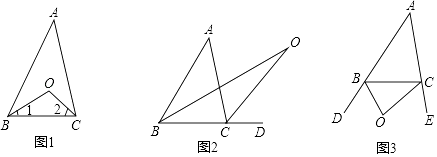
(1)探究二:如图2中,已知O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?并说明理由.
(2)探究二:如图3中,已知O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是必然事件的是( )
A.经过不断的努力,每个人都能获得“星光大道”年度总冠军
B.小冉打开电视,正在播放“奔跑吧,兄弟”
C.火车开到月球上
D.在十三名中国学生中,必有属相相同的
查看答案和解析>>
科目:初中数学 来源: 题型:
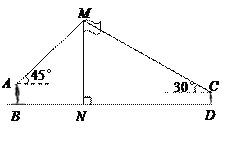
【题目】如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离AB=1.7m,看旗杆顶部![]() 的仰角为
的仰角为![]() ;小红的眼睛与地面的距离CD=1.5m,看旗杆顶部
;小红的眼睛与地面的距离CD=1.5m,看旗杆顶部![]() 的仰角为
的仰角为![]() .两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).请求出旗杆
.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).请求出旗杆![]() 的高度.(参考数据:
的高度.(参考数据: ![]() ,
, ![]() ,结果保留整数)
,结果保留整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com