
【题目】如图所示,![]() 个直角边长为3的等腰直角三角形
个直角边长为3的等腰直角三角形![]() ,
,![]() ……,斜边在同一直线上,设
……,斜边在同一直线上,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() …,
…,![]() 的面积为
的面积为![]() ,则
,则![]() _________________;
_________________;![]() _____________.
_____________.

【答案】![]()
![]()
【解析】
连接B1、B2、B3、B4、B5点,显然它们共线且平行于AC1,依题意可知△B1C1B2是等腰直角三角形,知道△B1B2D1与△C1AD1相似,求出相似比,根据三角形面积公式可得出S1,同理:B2B3:AC2=1:2,所以B2D2:D2C2=1:2,所以S2=![]() ,同样的道理,即可求出S3,S4…Sn.
,同样的道理,即可求出S3,S4…Sn.
∵n+1个边长为1的等腰三角形有一条边在同一直线上,
∴S△AB1C1=![]() ,
,
连接B1、B2、B3、B4、B5点,根据等腰三角形性质和平行线判定,它们共线且平行于AC1
∵∠B1C1B2=90°
∴A1B1∥B2C1
∴△B1C1B2是等腰直角三角形,且边长=1,
∴△B1B2D1∽△C1AD1,
∴B1D1:D1C1=1:1,
∴S1=![]() ,
,
故答案为:![]() ;
;
同理:B2B3:AC2=1:2,
∴B2D2:D2C2=1:2,
∴S2=![]() ,
,
同理:B3B4:AC3=1:3,
∴B3D3:D3C3=1:3,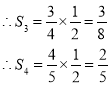 ,
,
…
∴Sn=![]()
故答案为:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图![]() 中,
中,![]() ,P是斜边AC上一个动点,以即为直径作
,P是斜边AC上一个动点,以即为直径作![]() 交BC于点D,与AC的另一个交点E,连接DE.
交BC于点D,与AC的另一个交点E,连接DE.
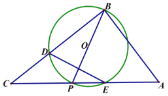
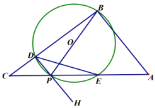
(1)当![]() 时,
时,
①若![]() ,求
,求![]() 的度数;
的度数;
②求证![]() ;
;
(2)当![]() ,
,![]() 时,
时,
①是含存在点P,使得![]() 是等腰三角形,若存在求出所有符合条件的CP的长;
是等腰三角形,若存在求出所有符合条件的CP的长;
②以D为端点过P作射线DH,作点O关于DE的对称点Q恰好落在![]() 内,则CP的取值范围为________.(直接写出结果)
内,则CP的取值范围为________.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 以上均不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.
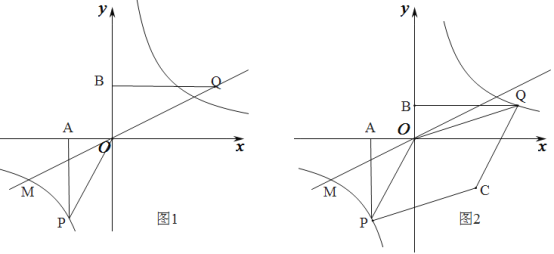
(1)写出正比例函数和反比例函数的关系式;
(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;
(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上)
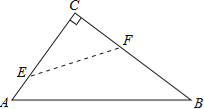
(1)若△CEF与△ABC相似.
①当AC=BC=2时,AD的长为 ;
②当AC=3,BC=4时,AD的长为 ;
(2)当点D是AB的中点时,△CEF与△ABC相似吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进某种商品时的单价是40元,根据市场调查:在一段时间内,销售单价是60元时,销售量是300件,而销售单价每涨1元,就会少售出10件.
(1)设该种商品的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润W元,并把结果填写在表格中:
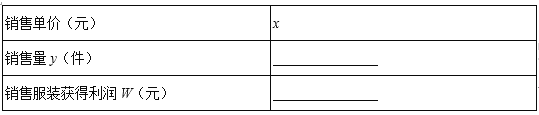
(2)在(1)的条件下,若商场获得了4000元销售利润,求该商品销售单价x应定为多少元?
(3)当定价多少时,该商场获得的最大利润,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两位同学利用灯光下的影子来测量一路灯A的高度,如图,当甲走到点C处时,乙测得甲直立身高CD与其影子长CE正好相等,接着甲沿BC方向继续向前走,走到点E处时,甲直立身高EF的影子恰好是线段EG,并测得EG=2.5m.已知甲直立时的身高为1.75m,求路灯的高AB的长.(结果精确到0.1m)
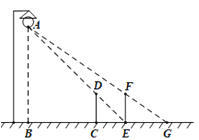
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1米,拱桥的跨度为10米,桥洞与水面的最大距离是5米,桥洞两侧壁上各有一盏距离水面4米的景观灯,两盏景观灯之间的水平距离为________米.
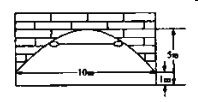
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com