
【题目】如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上)
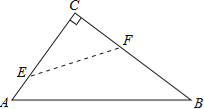
(1)若△CEF与△ABC相似.
①当AC=BC=2时,AD的长为 ;
②当AC=3,BC=4时,AD的长为 ;
(2)当点D是AB的中点时,△CEF与△ABC相似吗?请说明理由.
【答案】解:(1)①![]() 。
。
②![]() 或
或![]() 。
。
(2)当点D是AB的中点时,△CEF与△ABC相似。理由如下:
如答图3所示,连接CD,与EF交于点Q,
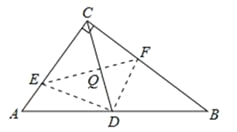
∵CD是Rt△ABC的中线,∴CD=DB=AB,∴∠DCB=∠B。
由折叠性质可知,∠CQF=∠DQF=90°,
∴∠DCB+∠CFE=90°。
∵∠B+∠A=90°,∴∠CFE=∠A。
又∵∠C=∠C,∴△CEF∽△CBA。
【解析】
(1)若△CEF与△ABC相似.
①当AC=BC=2时,△ABC为等腰直角三角形,如答图1所示,
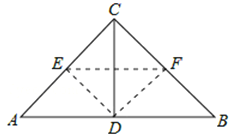
此时D为AB边中点,AD=![]() AC=
AC=![]() 。
。
②当AC=3,BC=4时,有两种情况:
(I)若CE:CF=3:4,如答图2所示,
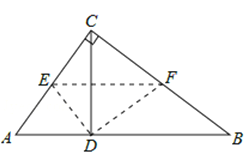
∵CE:CF=AC:BC,∴EF∥BC。
由折叠性质可知,CD⊥EF,
∴CD⊥AB,即此时CD为AB边上的高。
在Rt△ABC中,AC=3,BC=4,∴BC=5。
∴cosA=![]() 。∴AD=ACcosA=3×
。∴AD=ACcosA=3×![]() =
=![]() 。
。
(II)若CF:CE=3:4,如答图3所示.
∵△CEF∽△CAB,∴∠CEF=∠B。
由折叠性质可知,∠CEF+∠ECD=90°。
又∵∠A+∠B=90°,∴∠A=∠ECD,∴AD=CD。
同理可得:∠B=∠FCD,CD=BD。∴AD=BD。
∴此时AD=AB=![]() ×5=
×5=![]() .
.
综上所述,当AC=3,BC=4时,AD的长为![]() 或
或![]() 。
。
(2)当点D是AB的中点时,△CEF与△ABC相似.可以推出∠CFE=∠A,∠C=∠C,从而可以证明两个三角形相似。


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为 度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“上升数”是一个数中右边数字比左边数字大的自然数(如:34,568,2469等).任取一个两位数,是“上升数”的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司购进某种水果的成本为![]() 元/千克,经过市场调研发现,这种水果在未来
元/千克,经过市场调研发现,这种水果在未来![]() 天的销售价格
天的销售价格![]() (元/千克)与时间
(元/千克)与时间![]() (天)之间的函数关系式为
(天)之间的函数关系式为
 ,且其日销售量
,且其日销售量![]() (千克)与时间
(千克)与时间![]() (天)的关系如下表:
(天)的关系如下表:
时间 |
|
|
|
|
|
| … |
日销售量 |
|
|
|
|
|
| … |
![]() 已知
已知![]() 与
与![]() 之间的变化规律符合一次函数关系,试求在第
之间的变化规律符合一次函数关系,试求在第![]() 天的日销售量是多少?
天的日销售量是多少?
![]() 问哪一天的销售利润最大?最大日销售利润为多少?
问哪一天的销售利润最大?最大日销售利润为多少?
![]() 在实际销售的前
在实际销售的前![]() 天中,公司决定每销售
天中,公司决定每销售![]() 千克水果就捐赠
千克水果就捐赠![]() 元利润
元利润![]() 给“精准扶贫”对象.现发现:在前
给“精准扶贫”对象.现发现:在前![]() 天中,每天扣除捐赠后的日销售利润随时间
天中,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
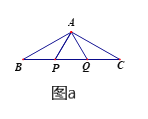
【题目】如图a,P、Q是△ABC的边BC上的两点,且△APQ为等边三角形,AB=AC,
(1)求证:BP=CQ.
(2)如图a,若∠BAC=120![]() ,AP=3,求BC的长.
,AP=3,求BC的长.
(3)若∠BAC=120![]() ,沿直线BC向右平行移动△APQ得到△A′P′Q′(如图b),A′Q′与AC交于点M.当点P移动到何处时,△AA′M≌△CQ′M?证明你的结论.
,沿直线BC向右平行移动△APQ得到△A′P′Q′(如图b),A′Q′与AC交于点M.当点P移动到何处时,△AA′M≌△CQ′M?证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店计划购进A、B两种型号的电动自行车共30辆,其中A型电动自行车不少于20辆,A、B两种型号电动自行车的进货单价分别为2500元、3000元,售价分别为2800元、3500元,设该商店计划购进A型电动自行车m辆,两种型号的电动自行车全部销售后可获利润y元.
(1)求出y与m之间的函数关系式;
(2)该商店如何进货才能获得最大利润?此时最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=mx+b的图象与反比例函数y=![]() 的图象交于A(3,1),B(﹣
的图象交于A(3,1),B(﹣![]() ,n)两点.
,n)两点.
(1)求该反比例函数的解析式;
(2)求n的值及该一次函数的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC沿EF对折,叠合后的图形如图所示.若∠A=60°,∠1=85°,则∠2的度数( )

A. 24°B. 25°C. 30°D. 35°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com