
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,CE⊥CD且CE=CD,连接EF. 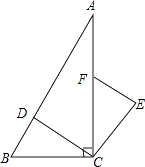
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
【答案】
(1)证明:∵∠ACB=90°,CE⊥CD,
∴∠BCD+∠DCA=90°=∠DCA+∠FCE,
∴∠BCD=∠FCE.
在△BCD和△FCE中, 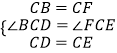 ,
,
∴△BCD≌△FCE(SAS)
(2)解:∵△BCD≌△FCE,
∴∠BDC=∠FEC.
∵EF∥CD,
∴∠DCE+∠FEC=180°,
又∵CE⊥CD,
∴∠FEC=180°﹣∠DCE=180°﹣90°=90°,
∴∠BDC=90°
【解析】(1)根据∠ACB=90°、CE⊥CD利用角的计算即可得出∠BCD=∠FCE,再结合CB=CF、CD=CE即可证出△BCD≌△FCE(SAS);(2)由(1)可得出∠BDC=∠FEC,由EF∥CD利用平行线的性质即可得出∠DCE+∠FEC=180°,再结合CE⊥CD即可得出结论.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角).


科目:初中数学 来源: 题型:
【题目】方程(x-1)(x+3)=12化为ax2+bx+c=0的形式后,a、b、c的值为( )
A.1、2、-15
B.1、-2、-15
C.-1、-2、-15
D.-1、2、-15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠ACB=90°,∠A=30°,DE垂直平分AC,D为垂足,交AB于E,连接CE. 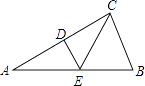
(1)求∠ECB的度数;
(2)若AB=10,求△BCE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图: 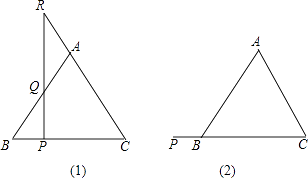
(1)P是等腰三角形ABC底边BC上的一个动点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R.请观察AR与AQ,它们有何关系?并证明你的猜想.
(2)如果点P沿着底边BC所在的直线,按由C向B的方向运动到CB的延长线上时,(1)中所得的结论还成立吗?请你在图(2)中完成图形,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C.△ABC中,∠A=50°,求∠DBA+∠DCA的度数. 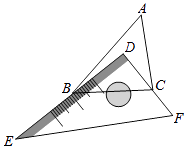
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com