
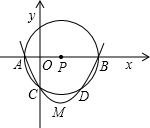
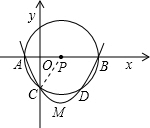
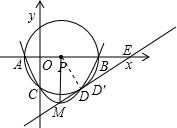
 (1998•黄冈)如图,直角坐标系中,O为坐标原点,A点坐标为(-3,0),B点坐标为(12,0),以AB为直径作⊙P与y轴的负半轴交于点C.抛物线y=ax2+bx+c经过A、B、C三点,其顶点为M点.
(1998•黄冈)如图,直角坐标系中,O为坐标原点,A点坐标为(-3,0),B点坐标为(12,0),以AB为直径作⊙P与y轴的负半轴交于点C.抛物线y=ax2+bx+c经过A、B、C三点,其顶点为M点.| 3 |
| 4 |
| 51 |
| 4 |
| PC2-OP2 |
|
|
| 1 |
| 6 |
| 3 |
| 2 |
| 1 |
| 6 |
| 3 |
| 2 |
| 1 |
| 6 |
| 9 |
| 2 |
| 75 |
| 8 |
| 9 |
| 2 |
| 75 |
| 8 |
| 9 |
| 2 |
| 75 |
| 8 |
|
|
| 3 |
| 4 |
| 51 |
| 4 |
| 3 |
| 4 |
| 51 |
| 4 |
| 75 |
| 8 |
| PE2+PM2 |
| 125 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
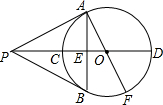 (1998•黄冈)如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于C、D,交AB于E,AF为⊙O的直径,下列结论:①∠ABP=∠AOP;②
(1998•黄冈)如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于C、D,交AB于E,AF为⊙O的直径,下列结论:①∠ABP=∠AOP;② |
| BC |
 |
| DF |
查看答案和解析>>
科目:初中数学 来源: 题型:
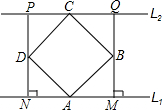 (1998•黄冈)如图,已知四边形ABCD是正方形,分别过A、C两点作l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、ND分别交l2于Q、P.求证:四边形PQMN是正方形.
(1998•黄冈)如图,已知四边形ABCD是正方形,分别过A、C两点作l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、ND分别交l2于Q、P.求证:四边形PQMN是正方形.查看答案和解析>>
科目:初中数学 来源: 题型:
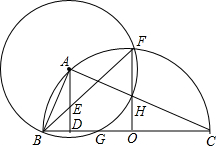 (1998•黄冈)如图,⊙O是△ABC的外接圆,BC是直径,以顶点A为圆心,AB长为半径的圆交⊙O于F点,交BC于G点(AB<OB).AD⊥BC于D,AD与BF交于E点,OF交⊙A于H点.求证:
(1998•黄冈)如图,⊙O是△ABC的外接圆,BC是直径,以顶点A为圆心,AB长为半径的圆交⊙O于F点,交BC于G点(AB<OB).AD⊥BC于D,AD与BF交于E点,OF交⊙A于H点.求证:| FH |
| 2AE |
| BF |
| BC |
查看答案和解析>>
科目:初中数学 来源:2009年福建省三明市大田二中自主招生数学模拟试卷(3)(解析版) 题型:填空题
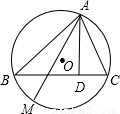
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com