
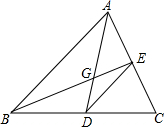
 如图所示,在△ABC中,中线AD、BE交于G,△ABC面积为1,则△BDG的面积为$\frac{1}{6}$,若连接DE,则△CDE的面积为$\frac{1}{4}$,△ABG的面积为$\frac{1}{3}$,△DEG的面积为$\frac{1}{12}$.
如图所示,在△ABC中,中线AD、BE交于G,△ABC面积为1,则△BDG的面积为$\frac{1}{6}$,若连接DE,则△CDE的面积为$\frac{1}{4}$,△ABG的面积为$\frac{1}{3}$,△DEG的面积为$\frac{1}{12}$. 分析 根据三角形中位线定理得到DE∥AB,DE=$\frac{1}{2}$AB,根据相似三角形的性质得到S△DEC:S△ABC=S△DEG:S△AGB=1:4,根据重心的性质得到S△ABC=3S△AGB,计算得到答案
解答 解:∵AD、BE是△ABC的中线,
∴DE∥AB,DE=$\frac{1}{2}$AB,
∴S△DEC:S△ABC=S△DEG:S△AGB=1:4,
∵S△ABC=1,
∴S△DEC=$\frac{1}{4}$,
∵AD是BC边上的中线,
∴S△ABC=2S△ADC,
∵G是重心,
∴AG=2DG,
∴S△AGB=2S△GEA,
∴S△ABC=3S△AGB,
∴S△ABG=$\frac{1}{3}$,
∴S△ABC:S△DEG=12:1,
∴S△DEG=$\frac{1}{12}$,
∴S△AEG=S△DBG=$\frac{1}{6}$.
故答案为$\frac{1}{6}$,$\frac{1}{4}$,$\frac{1}{3}$,$\frac{1}{12}$.
点评 本题考查了三角形的面积,还考查了三角形的重心的概念和性质,掌握三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍是解题的关键,注意相似三角形的面积比等于相似比的平方.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com