
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点H,点G在弧BD上,连接AG,交CD于点K,过点G的直线交CD延长线于点E,交AB延长线于点F,且EG=EK.
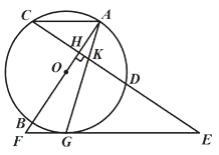
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为13,CH=12,AC∥EF,求OH和FG的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)连接OG,首先证明∠EGK=∠EKG,再证明∠HAK+∠KGE=90°,进而得到∠OGA+∠KGE=90°即GO⊥EF,进而证明EF是⊙O的切线;
(2)连接CO,利用勾股定理计算出HO的长,然后可得tan∠CAH=tan∠F=![]() ,再利用三角函数在Rt△OGF中计算出FG的长.
,再利用三角函数在Rt△OGF中计算出FG的长.
试题解析:(1)证明:连接OG,
∵弦CD⊥AB于点H,
∴∠AHK=90°,
∴∠HKA+∠KAH=90°,
∵EG=EK,
∴∠EGK=∠EKG,
∵∠HKA=∠GKE,
∴∠HAK+∠KGE=90°,
∵AO=GO,
∴∠OAG=∠OGA,
∴∠OGA+∠KGE=90°,
∴GO⊥EF,
∴EF是⊙O的切线;
(2)解:连接CO,在Rt△OHC中,
∵CO=13,CH=12,
∴HO=5,
∴AH=8,
∵AC∥EF,
∴∠CAH=∠F,
∴tan∠CAH=tan∠F=![]() ,
,
在Rt△OGF中,∵GO=13,
∴FG=![]() .
.
考点: 1.切线的判定,2.解直角三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+2x与直线y= ![]() 交于A,B两点,与直线x=2交于点P,将抛物线沿着射线AB平移
交于A,B两点,与直线x=2交于点P,将抛物线沿着射线AB平移![]() 个单位.
个单位.

(1)平移后的抛物线顶点坐标为_______;
(2)在整个平移过程中,点P经过的路程为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
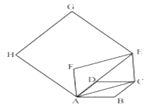
【题目】如图,边长为1的菱形![]() 中,
中,![]() ,连结对角线
,连结对角线![]() ,以
,以![]() 为边做第二个菱形
为边做第二个菱形![]() ,
,![]() .连结
.连结![]() ,再以
,再以![]() 为边做第三个菱形
为边做第三个菱形![]() ,使
,使![]() …按此规律所作的第2015个菱形的边长是__________.
…按此规律所作的第2015个菱形的边长是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
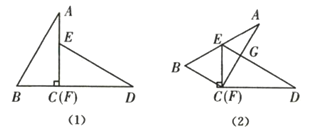
【题目】如图,已知![]() 与
与![]() 是两个全等的直角三角形,量得它们的斜边长为
是两个全等的直角三角形,量得它们的斜边长为![]() ,较小锐角为
,较小锐角为![]() ,将这两个三角形摆成如图(1)所示的形状,使点
,将这两个三角形摆成如图(1)所示的形状,使点![]() 、
、![]() 、
、![]() 、
、![]() 在同一条直线上,且点
在同一条直线上,且点![]() 与点
与点![]() 重合,将图(1)中的
重合,将图(1)中的![]() 绕点
绕点![]() 顺时针方向旋转到图(2)的位置,点
顺时针方向旋转到图(2)的位置,点![]() 在边
在边![]() 上,
上,![]() 交
交![]() 于点
于点![]() ,则线段
,则线段![]() 的长为______
的长为______![]() .(保留根号)
.(保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆桌面正上方的灯泡发出的光线照射桌面后,在地面上形成阴影(圆形).已知灯泡距离地面2.4m,桌面距离地面0.8m(桌面厚度不计算),若桌面的面积是1.2m,则地面上的阴影面积是__________m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有3个黑球和若干白球,它们除颜色外都相同.在不允许将球倒出来数的前提下,小明为估计其中白球数,采用如下办法:随机从中摸出一球,记下颜色后放回袋中,充分摇匀后,再随机摸出一球,记下颜色,…不断重复上述过程.小明共摸100次,其中20次摸到黑球.根据上述数据,小明估计口袋中白球大约有( )
A. 10个 B. 12 个 C. 15 个 D. 18个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小冬与小夏是某中学篮球队的队员,在最近五场球赛中的得分如下表所示:
第一场 | 第二场 | 第三场 | 第四场 | 第五场 | |
小冬 |
|
|
|
|
|
小夏 |
|
|
|
|
|
(1)根据上表所给的数据,填写下表:
平均数 | 中位数 | 众数 | 方差 | |
小冬 |
|
|
| |
小夏 |
|
|
|
(2)根据以上信息,若教练选择小冬参加下一场比赛,教练的理由是什么?
(3)若小冬的下一场球赛得分是![]() 分,则在小冬得分的四个统计量中(平均数、中位数、众数与方差)哪些发生了改变,改变后是变大还是变小?(只要回答是“变大”或“变小”)(
分,则在小冬得分的四个统计量中(平均数、中位数、众数与方差)哪些发生了改变,改变后是变大还是变小?(只要回答是“变大”或“变小”)(![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com