
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源:2016-2017学年四川达县万家中学下学期九年级第一次月考数学试卷(解析版) 题型:单选题
在“百度”搜索引擎中输入“初中数学教育”,能搜索到与之相关的网页约为8 680 000个,将这个数用科学记数法表示为( )
A. 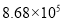 B.
B. 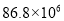 C.
C. 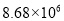 D.
D. 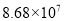
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省八年级下学期第一次月考数学试卷(解析版) 题型:填空题
在平行四边形ABCD中,∠BAD的平分线AE交BC于点E,且BE=3,若平行四边形ABCD的周长是16,则EC等于____________.
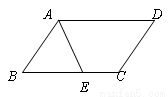
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
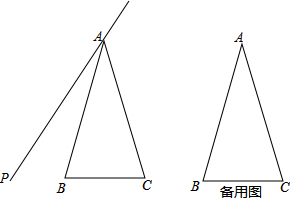
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
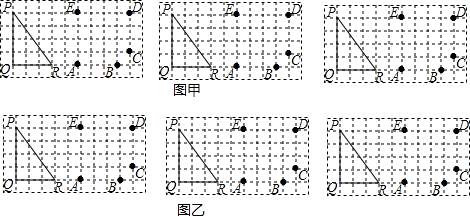
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
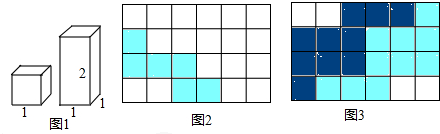
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com