
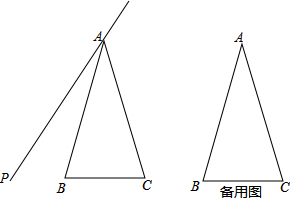
���� ��1���ٰ�Ҫ�����ɣ�
�ڸ��ݵ�B����ֱ��AP�ĶԳƵ�Ϊ��D���õ�AP��ֱƽ��BD�����ô�ֱƽ���ߵ����ʣ�֤����ACDΪ�ȱ������Σ����ɵõ���ACD=60�㣻
��DE=2BF������EB������AP��ֱƽ��BD���õ�ED=EB�����õȱ߶ԵȽǵõ���3=��4�����õ��������ε����������3=��4=15�㣬��5=30�㣬����ΪAD=AC��ABƽ�֡�DAC������AB��DC�����ɵõ�EB=2BF������ED=2BF��
��2������ͼ�Σ�������������ۣ���AE=AFʱ����AE=EFʱ����EF=AFʱ��
��� �⣺��1������ͼ1��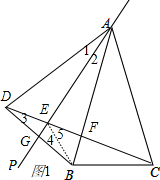
�ڡ�B��D����AP�Գƣ�
��AP��ֱƽ��BD��a=15�㣬
��AD=AB����1=��2=15�㣬
�ߡ�BAC=30�㣬
���DAC=��1+��2+��BAC=60�㣬
��AC=AB��
��AC=AD��
���ACDΪ�ȱ�������
���ACD=60�㣮
��DE=2BF��
֤��������EB��
��AP��ֱƽ��BD��
��ED=EB��
���3=��4��
��AB=AD����DAB=30�㣬
���ADB=75�㣬
�֡�ADC=60�㣬
���3=��4=15�㣬
���5=30�㣬
��AD=AC��ABƽ�֡�DAC��
��AB��DC��
��EB=2BF��
��ED=2BF��
��2����ͼ2��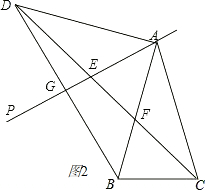
��AD=AC��
���DAC�ǵ���������
���ADC=��180��-2a-30�㣩��2=75��-a��
���AEF=��ADC+��DAE=75��-a+a=75�㣬
��AE=AFʱ����EAF=a=180��-75���2=180��-150��=30�㣻
��AE=EFʱ����EAF=a=��180��-75�㣩��=52.5�㣻
��EF=AFʱ����AEF=��EAF=a=75�㣨��ȥ����
�ʴ�Ϊ��30���52.5�㣮
���� ���⿼������ͼ���������Ĺؼ�������ͼ�Σ����ô�ֱƽ���ߵ����ʣ����������ε����ʣ��ȱ������ε����ʽ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ�꽭��ʡ��ͨ�����꼶3���¿���ѧ�Ծ��������棩 ���ͣ��ж���
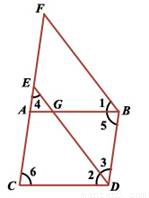
��֪����ͼ����1 =��2����3 =��4����5 =��6.��֤��ED��FB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ���Ĵ����������ѧ��ѧ�ھ��꼶��һ���¿���ѧ�Ծ��������棩 ���ͣ���ѡ��
������x��һԪ���η���kx2��2x��1=0��ʵ��������k��ȡֵ��Χ�ǣ� ��
A. k��-1��k��0 B. k��-1 C. k��1 D. k��1��k��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�꽭��ʡ���꼶��ѧ�ڵ�һ���¿���ѧ�Ծ��������棩 ���ͣ������
��֪������ABCD�ı߳�Ϊ1���ֱ���B��DΪԲ�ģ���aΪ�뾶��������ͼ��ʾ������Ӱ���ֵ����Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�꽭��ʡ���꼶��ѧ�ڵ�һ���¿���ѧ�Ծ��������棩 ���ͣ������
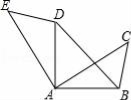
��ͼ������ABC�Ƶ�A��ʱ����ת�ĵ���ADE����C�͵�E�Ƕ�Ӧ�㣬����CAE=90�㣬AB=1����BD= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
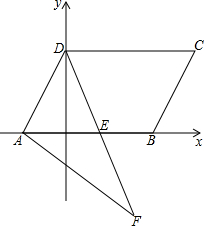 ��ͼ��ƽ��ֱ������ϵ�У���A��B����x���ϣ�OA=2��OB=3�����߶�AB����ƽ��3����λ��������ƽ��2����λ���õ��߶�CD������AD��BC��
��ͼ��ƽ��ֱ������ϵ�У���A��B����x���ϣ�OA=2��OB=3�����߶�AB����ƽ��3����λ��������ƽ��2����λ���õ��߶�CD������AD��BC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com