
分析 (1)原式第一项化为最简二次根式,第二项利用负指数幂法则计算,第三项利用特殊角的三角函数值计算,最后一项利用零指数幂法则计算即可得到结果;
(2)原式第二项约分后,两项通分并利用同分母分式的减法法则计算得到最简结果,把已知等式代入计算即可求出值.
解答 解:(1)原式=2$\sqrt{3}$-3×$\frac{\sqrt{3}}{3}$+2×$\frac{\sqrt{3}}{2}$-1=2$\sqrt{3}$-1;
(2)原式=$\frac{1}{a+1}$-$\frac{1}{(a+1)(a-1)}$•$\frac{(a-1)^{2}}{a}$=$\frac{1}{a+1}$-$\frac{a-1}{a(a+1)}$=$\frac{a-a+1}{a(a+1)}$=$\frac{1}{{a}^{2}+a}$,
当a2+a=3时,原式=$\frac{1}{3}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源:2016-2017学年四川达县万家中学下学期九年级第一次月考数学试卷(解析版) 题型:解答题
如图,在网格图中建立平面直角坐标系, 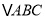 的顶点坐标为
的顶点坐标为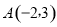 、
、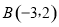 、
、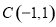 .
.
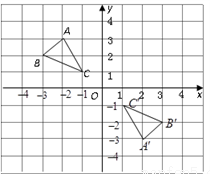
(1)若将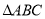 向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的
向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的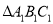 ;
;
(2)画出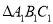 绕C1顺时针方向旋转900后得到的
绕C1顺时针方向旋转900后得到的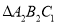 ;
;
(3)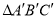 与
与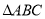 是中心对称图形,请写出对称中心的坐标: ;并计算
是中心对称图形,请写出对称中心的坐标: ;并计算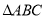 的面积: .
的面积: .
(4)在坐标轴上是否存在P点,使得△PAB与△CAB的面积相等,若有,则求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
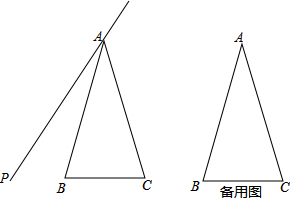
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
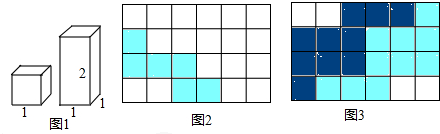
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
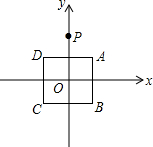 正方形ABCD在坐标系中位置如图所示,作点P(0,2)关于点A的对称点P1,点P1关于点B的对称点P2,点P2关于点C的对称点P3,点P3关于点D的对称点P4,…,按此操作下去,则点P2014的坐标为( )
正方形ABCD在坐标系中位置如图所示,作点P(0,2)关于点A的对称点P1,点P1关于点B的对称点P2,点P2关于点C的对称点P3,点P3关于点D的对称点P4,…,按此操作下去,则点P2014的坐标为( )| A. | (0,2) | B. | (2,0) | C. | (0,-2) | D. | (-2,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a3•a2=a6 | B. | a3÷a2=a${\;}^{\frac{3}{2}}$ | C. | a3-a2=a | D. | (a+1)2=a2+2a+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 月均用水量x/m3 | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 | x>20 |
| 频数/户 | 12 | 20 | 3 | ||
| 频率 | 0.12 | 0.07 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com