
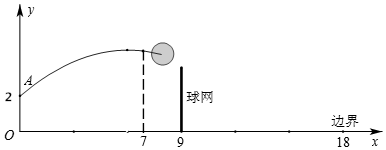
分析 (1)根据抛物线过点(0,2)代入抛物线解析式即可解答本题;
(2)先判断,再说明理由,根据题意可以解答本题;
(3)根据题意可以得到相应的关系式,从而可以解答本题.
解答 解:(1)当h=2.7时,
y=a(x-7)2+2.7,
∵此抛物线过点(0,2),
∴2=a(0-7)2+2.7,
解得,a=-$\frac{1}{70}$,
即当h=2.7时,y与x的关系式是y=-$\frac{1}{70}$(x-7)2+2.7;
(2)当h=2.7时,球能越过球网,球会出界,
理由:将x=9代入y=-$\frac{1}{70}$(x-7)2+2.7,得
y=-$\frac{1}{70}$(9-7)2+2.7≈2.643,
∵2.643>2.24,
∴当h=2.7时,球能越过球网,
将y=0代入y=-$\frac{1}{70}$(x-7)2+2.7,的x=-6.75(舍去)或x=20.75,
∵20.75>18,
∴当h=2.7时,球会出界,
由上可得,当h=2.7时,球能越过球网,球会出界;
(3)由题意可得,
$\left\{\begin{array}{l}{a(18-7)^{2}+h<0}\\{a(9-7)^{2}+h>2.24}\\{2=a(0-7)^{2}+h}\end{array}\right.$,
解得,h>3.36
即球一定能越过球网,又不出边界,h的取值范围是h>3.36.
点评 本题考查二次函数的应用,解题的关键是明确题意,找出所求问题需要的条件.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
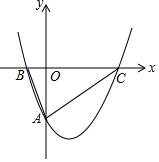 如图,已知抛物线y=$\frac{1}{2}$x2-x-4与x轴交于B,C,与y轴交于A,点P是抛物线上一点,且∠ACP+∠OAB=∠ACB,求点P的坐标.
如图,已知抛物线y=$\frac{1}{2}$x2-x-4与x轴交于B,C,与y轴交于A,点P是抛物线上一点,且∠ACP+∠OAB=∠ACB,求点P的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
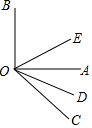 如图所示,已知∠AOB=90°,∠AOC为锐角,OD平分∠AOC,OE平分∠BOC.
如图所示,已知∠AOB=90°,∠AOC为锐角,OD平分∠AOC,OE平分∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
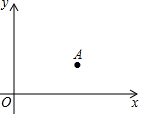 如图,点A的坐标为(3,2),点B与点A关于x轴对称,AB交x轴于点C.
如图,点A的坐标为(3,2),点B与点A关于x轴对称,AB交x轴于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是半圆O的直径,射线AM、BN分别与半圆O相切于点A、B,点E在半圆上,点D在射线AM上,连接DE并延长交射线BN于点C,连接AE并延长交射线BN于点G.
如图,AB是半圆O的直径,射线AM、BN分别与半圆O相切于点A、B,点E在半圆上,点D在射线AM上,连接DE并延长交射线BN于点C,连接AE并延长交射线BN于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
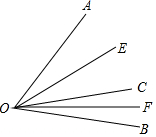 已知,如图,OC是∠AOB内部一条射线,∠AOB=60°,OE、OF分别是∠AOC、∠COB的角平分线,求∠EOF的度数?如果设∠AOB=β,其他条件不变,你能猜测出∠EOF的大小吗?请用一句简洁的话表述你发现的规律.
已知,如图,OC是∠AOB内部一条射线,∠AOB=60°,OE、OF分别是∠AOC、∠COB的角平分线,求∠EOF的度数?如果设∠AOB=β,其他条件不变,你能猜测出∠EOF的大小吗?请用一句简洁的话表述你发现的规律.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com