


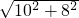 =2
=2 ,
, (DC+AB)•BC=
(DC+AB)•BC= (10+16)×8=104,
(10+16)×8=104, DC•BC=
DC•BC= ×10×8=40,
×10×8=40, BD•x=S梯形ABCD-S△BCD=104-40=64,
BD•x=S梯形ABCD-S△BCD=104-40=64,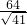 =
=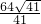 .
.

 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
| DF | FC |
查看答案和解析>>
科目:初中数学 来源: 题型:
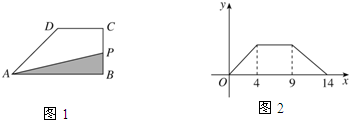
查看答案和解析>>
科目:初中数学 来源: 题型:
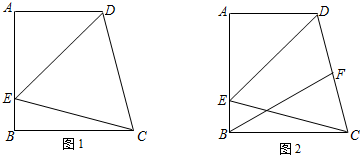
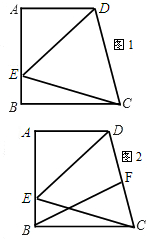 如图1所示,在直角梯形ABCD中,AD∥BC,∠DCB=75°,AB⊥BC,以CD为一边的等边△DCE的另一顶点E在腰AB上.
如图1所示,在直角梯形ABCD中,AD∥BC,∠DCB=75°,AB⊥BC,以CD为一边的等边△DCE的另一顶点E在腰AB上.查看答案和解析>>
科目:初中数学 来源:2012届浙江省湖州市环渚学校九年级第二次月考数学试卷(带解析) 题型:单选题
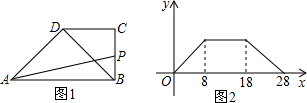
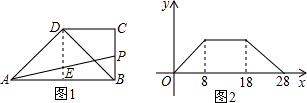
如图甲所示,在直角梯形ABCD中,AB∥DC, .动点P从点B出发,沿梯形的边由B→C→D→A运动.设点P运动的路程为x,△ABP的面积为y.把y看作x的函数,函数的图像如图乙所示,则△ABC的面积为
.动点P从点B出发,沿梯形的边由B→C→D→A运动.设点P运动的路程为x,△ABP的面积为y.把y看作x的函数,函数的图像如图乙所示,则△ABC的面积为 
| A.10 | B.16 | C.18 | D.32 |
查看答案和解析>>
科目:初中数学 来源:2013届广东省江门市福泉奥林匹克学校九年级3月份质量检测数学试卷(带解析) 题型:单选题
如图甲所示,在直角梯形ABCD中,AB∥DC, .动点P从点B出发,沿梯形的边由B→C→D→A运动.设点P运动的路程为x,△ABP的面积为y.把y看作x的函数,函数的图像如图乙所示,则△ABC的面积为( )
.动点P从点B出发,沿梯形的边由B→C→D→A运动.设点P运动的路程为x,△ABP的面积为y.把y看作x的函数,函数的图像如图乙所示,则△ABC的面积为( ) 
| A.10 | B.16 | C.18 | D.32 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com