
【题目】如图,直线y=mx与双曲线y=![]() 相交于A、B两点,A点的坐标为(1,2)
相交于A、B两点,A点的坐标为(1,2)
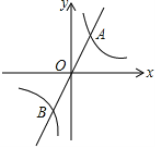
(1)求反比例函数的表达式;
(2)根据图象直接写出当mx>![]() 时,x的取值范围;
时,x的取值范围;
(3)计算线段AB的长.
【答案】(1)反比例函数的表达式是y=![]() ;(2)-1<x<0或x>1;(3)2
;(2)-1<x<0或x>1;(3)2![]() .
.
【解析】
试题分析:(1)把A的坐标代入反比例函数的解析式即可求出答案;
(2)求出直线的解析式,解组成的方程组求出B的坐标,根据A、B的坐标结合图象即可得出答案;
(3)根据A、B的坐标.利用勾股定理分别求出OA、OB,即可得出答案.
试题解析:(1)把A(1,2)代入y=![]() 得:k=2,
得:k=2,
即反比例函数的表达式是y=![]() ;
;
(2)把A(1,2)代入y=mx得:m=2,
即直线的解析式是y=2x,
解方程组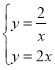
得出B点的坐标是(-1,-2),
∴当mx>![]() 时,x的取值范围是-1<x<0或x>1;
时,x的取值范围是-1<x<0或x>1;
(3)过A作AC⊥x轴于C,
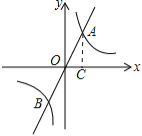
∵A(1,2),
∴AC=2,OC=1,
由勾股定理得:AO=![]() ,
,
同理求出OB=![]() ,
,
∴AB=2![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,小明将一张长为4、宽为3的矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用点F表示).
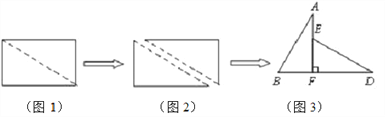
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
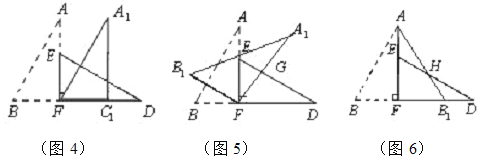
(1)将图3中的△ABF沿BD向右平移到图4中![]() 的位置,其中点B与点F 重合,请你求出平移的距离 ;
的位置,其中点B与点F 重合,请你求出平移的距离 ;
(2)在图5中若∠GFD=60°,则图3中的△ABF绕点 按 方向旋转 到图5的位置;
(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,试问:△AEH和△HB1D的面积大小关系.说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解居民用水情况,在某小区随机抽查了15户家庭的月用水量,结果如下表:
月用水量(吨) | 4 | 5 | 6 | 8 | 9 |
户数 | 2 | 5 | 4 | 3 | 1 |
则这15户家庭的月用水量的众数与中位数分别为( )
A.9、6
B.6、6
C.5、6
D.5、5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人从少年宫出发,沿相同的路线分别以不同的速度匀速跑向体育馆,甲先跑一段路程 后,乙开始出发,当乙超出甲 150 米时,乙停在原地等候甲,两人相遇后乙又继续以原来的速度跑向体育馆.如图所示是甲、乙两人在跑步的全过程中经过的路程 y(米)与甲出发的时间 x(秒)之间关系的图象.
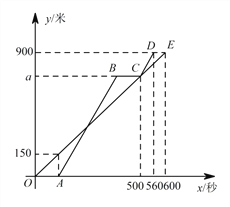
(1) 在跑步的全过程中,甲一共跑了 米,甲的速度为 米/秒.
(2) 求图中标注的 a 的值及乙跑步的速度.
(3) 乙在途中等候了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点E、D分别从A、C出发,沿AC,CB方向以相同的速度在线段AC,CB上运动,AD、BE相交于F点. 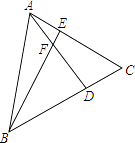
(1)求证:△ABE≌△CAD;
(2)当E、D运动时,∠BFD大小是否发生改变?若不变求其大小,若改变求其变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ACB中,∠ACB=90°,∠ABC=30°,AC=1,点D为AC上一动点,连接BD,以BD为边作等边△BDE,设CD=n. 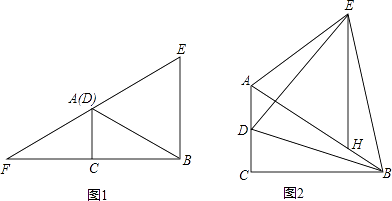
(1)当n=1时,EA的延长线交BC的延长线于F,则AF=;
(2)当0<n<1时,如图2,在BA上截取BH=AD,连接EH.
①设∠CBD=x,用含x的式子表示∠ADE和∠ABE.
②求证:△AEH为等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆和B型车b辆,一次运完,且每辆车都满载货物.根据以上信息解答下列问题:
(1)1辆A型车和1辆B型车载满货物一次分别可运货物多少吨?
(2)请帮助物流公司设计租车方案
(3)若A型车每辆车租金每次100元,B型车每辆车租金每次120元.请选出最省钱的租车方案,并求出最少的租车费.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com