
【题目】如图1,把一张长方形的纸片ABCD沿对角线BD折叠,点C落在E处,BE交AD于点F. 
(1)求证:FB=FD;
(2)如图2,连接AE,求证:AE∥BD; 
(3)如图3,延长BA,DE相交于点G,连接GF并延长交BD于点H,求证:GH垂直平分BD. 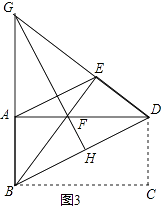
【答案】
(1)证明:∵△BCD≌△BED,
∴∠DBC=∠EBD,
又∵四边形ABCD是长方形,
∴AD∥BC,
∴∠ADB=∠DBC,
∴∠ADB=∠EBD,
∴BF=DF
(2)证明:∵四边形ABCD是长方形,
∴AD=BC=BE,
又∵FB=FD,
∴FA=FE,
∴∠FAE=∠FEA,
又∵∠AFE=∠BFD,且2∠AEF+∠AFE=2∠FBD+∠BFD=180°,
∴∠AEF=∠FBD,
∴AE∥BD
(3)证明:∵四边形ABCD是长方形,
∴AD=BC=BE,AB=CD=DE,BD=DB,
在△ABD与△EDB中,
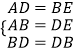
∴△ABD≌△EDB(SSS),
∴∠ABD=∠EDB,
∴GB=GD,
又∵FB=FD,
∴GF是BD的垂直平分线,即GH垂直平分BD
【解析】(1)由折叠的性质可得到△ABD≌△EDB,那么∠ADB=∠EBD,所以BF=DF;(2)根据长方形的性质可得和三角形内角和定理可得∠AEF=∠FBD,再根据平行线的判定即可求解;(3)先SSS证明△ABD≌△EDB,再根据全等三角形的性质和垂直平分线的性质即可求解.
【考点精析】本题主要考查了翻折变换(折叠问题)的相关知识点,需要掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
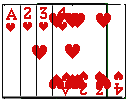
【题目】将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面上,从中随机抽取两张.
(1)用画树状图或列表的方法,列出抽得扑克牌上所标数字的所有可能组合;
(2)求抽得的扑克牌上的两个数字之积的算术平方根为有理数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算(-3xy2)·(2y2-xyz+1)的结果是( )
A. -3xy4+32y3+3xy2 B. -6xy4+3x2y3z-3xy2
C. -6xy4-3x2y3z-3xy2 D. -6xy4+3x2y2z
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2-8ax(a<0)的图像与x轴的正半轴交于点A,它的顶点为P.点C为y轴正半轴上一点,直线AC与该图像的另一交点为B,与过点P且垂直于x轴的直线交于点D,且CB:AB=1:7.
(1)求点A的坐标及点C的坐标(用含a的代数式表示);
(2)连接BP,若△BDP与△AOC相似(点O为原点),求此二次函数的关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
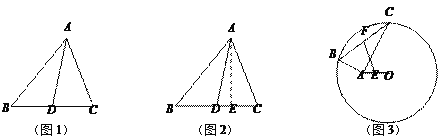
【题目】阅读理解:小明热爱数学,在课外书上看到了一个有趣的定理——“中线长定理”:三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍.如图1,在△ABC中,点D为BC的中点,根据“中线长定理”,可得:
AB2+AC2=2AD2+2BD2.
小明尝试对它进行证明,部分过程如下:
解:过点A作AE⊥BC于点E,如图2,在Rt△ABE中,AB2=AE2+BE2,
同理可得:AC2=AE2+CE2,AD2=AE2+DE2,
为证明的方便,不妨设BD=CD=x,DE=y,
∴AB2+AC2=AE2+BE2+AE2+CE2=……
(1)请你完成小明剩余的证明过程;
理解运用:
(2) ① 在△ABC中,点D为BC的中点,AB=6,AC=4,BC=8,则AD=_______;
② 如图3,⊙O的半径为6,点A在圆内,且OA=2![]() ,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为________;
,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为________;
拓展延伸:
(3)小明解决上述问题后,联想到《能力训练》上的题目:如图4,已知⊙O的半径为5![]() ,以A(3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.请你利用上面的方法和结论,求出AD长的最大值.
,以A(3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.请你利用上面的方法和结论,求出AD长的最大值.
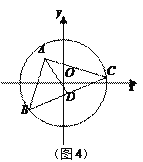
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,如图1,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面为矩形EFGH,如图2.设小正方形的边长为x厘米.
(1)当矩形纸板ABCD的一边长为90厘米时,求纸盒的侧面积的最大值;
(2)当EH:EF=7:2,且侧面积与底面积之比为9:7时,求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( ) 
A.带①去
B.带②去
C.带③去
D.带①和②去
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com