
 Èçͼ£¬ÒÑÖª¶þ´Îº¯ÊýL1£ºy=ax2-2ax+a+3£¨a£¾0£©ºÍ¶þ´Îº¯ÊýL2£ºy=-a£¨x+1£©2+1£¨a£¾0£©Í¼ÏóµÄ¶¥µã·Ö±ðΪM£¬N£¬ÓëyÖá·Ö±ð½»ÓÚµãE£¬F£®
Èçͼ£¬ÒÑÖª¶þ´Îº¯ÊýL1£ºy=ax2-2ax+a+3£¨a£¾0£©ºÍ¶þ´Îº¯ÊýL2£ºy=-a£¨x+1£©2+1£¨a£¾0£©Í¼ÏóµÄ¶¥µã·Ö±ðΪM£¬N£¬ÓëyÖá·Ö±ð½»ÓÚµãE£¬F£®·ÖÎö £¨1£©°Ñ¶þ´Îº¯ÊýL1£ºy=ax2-2ax+a+3»¯³É¶¥µãʽ£¬¼´¿ÉÇóµÃ×îСֵ£¬·Ö±ðÇóµÃ¶þ´Îº¯ÊýL1£¬L2µÄyÖµËæ×ÅxµÄÔö´ó¶ø¼õСµÄxµÄÈ¡Öµ£¬´Ó¶øÇóµÃ¶þ´Îº¯ÊýL1£¬L2µÄyֵͬʱËæ×ÅxµÄÔö´ó¶ø¼õСʱ£¬xµÄÈ¡Öµ·¶Î§£»
£¨2£©ÏÈÇóµÃE¡¢FµãµÄ×ø±ê£¬×÷MG¡ÍyÖáÓÚG£¬ÔòMG=1£¬×÷NH¡ÍyÖáÓÚH£¬ÔòNH=1£¬´Ó¶øÇóµÃMG=NH=1£¬È»ºóÖ¤µÃ¡÷EMG¡Õ¡÷FNH£¬¡ÏMEF=¡ÏNFE£¬EM=NF£¬½ø¶øÖ¤µÃEM¡ÎNF£¬´Ó¶øµÃ³öËıßÐÎENFMÊÇƽÐÐËıßÐΣ»
£¨3£©×÷MNµÄ´¹Ö±Æ½·ÖÏߣ¬½»MNÓÚD£¬½»xÖáÓÚA£¬ÏÈÇóµÃDµÄ×ø±ê£¬¼Ì¶øÇóµÃMNµÄ½âÎöʽ£¬½ø¶ø¾Í¿ÉÇóµÃÖ±ÏßADµÄ½âÎöʽ£¬Áîy=0£¬ÇóµÃAµÄ×ø±ê£¬¸ù¾Ý¶Ô³ÆÖá´Ó¶øÇóµÃÁíÒ»¸ö½»µãµÄ×ø±ê£¬¾Í¿ÉÇóµÃ·½³Ì-a£¨x+1£©2+1=0µÄ½â£®
½â´ð 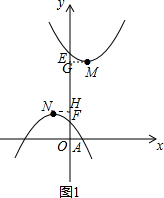 ½â£º£¨1£©¡ß¶þ´Îº¯ÊýL1£ºy=ax2-2ax+a+3=a£¨x-1£©2+3£¬
½â£º£¨1£©¡ß¶þ´Îº¯ÊýL1£ºy=ax2-2ax+a+3=a£¨x-1£©2+3£¬
¡à¶¥µãM×ø±êΪ£¨1£¬3£©£¬
¡ßa£¾0£¬
¡àº¯Êýy=ax2-2ax+a+3£¨a£¾0£©µÄ×îСֵΪ3£¬
¡ß¶þ´Îº¯ÊýL1µÄ¶Ô³ÆÖáΪx=1£¬µ±x£¼1ʱ£¬yËæxµÄÔö´ó¶ø¼õС£»
¶þ´Îº¯ÊýL2£ºy=-a£¨x+1£©2+1µÄ¶Ô³ÆÖáΪx=-1£¬µ±x£¾-1ʱ£¬yËæxµÄÔö´ó¶ø¼õС£»
¡àµ±¶þ´Îº¯ÊýL1£¬L2µÄyֵͬʱËæ×ÅxµÄÔö´ó¶ø¼õСʱ£¬xµÄÈ¡Öµ·¶Î§ÊÇ-1¡Üx¡Ü1£»
¹Ê´ð°¸Îª£º3£¬-1¡Üx¡Ü1£®
£¨2£©Óɶþ´Îº¯ÊýL1£ºy=ax2-2ax+a+3¿ÉÖªE£¨0£¬a+3£©£¬
Óɶþ´Îº¯ÊýL2£ºy=-a£¨x+1£©2+1=-a2x-2ax-a+1¿ÉÖªF£¨0£¬-a+1£©£¬
¡ßM£¨1£¬3£©£¬N£¨-1£¬1£©£¬
¡àEF=MN=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$£¬
¡àa+3-£¨-a+1£©=2$\sqrt{2}$£¬
¡àa=$\sqrt{2}$-1£¬
×÷MG¡ÍyÖáÓÚG£¬ÔòMG=1£¬×÷NH¡ÍyÖáÓÚH£¬ÔòNH=1£¬
¡àMG=NH=1£¬
¡ßEG=a+3-3=a£¬FH=1-£¨-a+1£©=a£¬
¡àEG=FH£¬
ÔÚ¡÷EMGºÍ¡÷FNHÖУ¬
$\left\{\begin{array}{l}{EG=FH}\\{¡ÏEGM=¡ÏFHN}\\{MG=NH}\end{array}\right.$£¬
¡à¡÷EMG¡Õ¡÷FNH£¨SAS£©£¬
¡à¡ÏMEF=¡ÏNFE£¬EM=NF£¬
¡àEM¡ÎNF£¬
¡àËıßÐÎENFMÊÇƽÐÐËıßÐΣ»
¡ßEF=MN£¬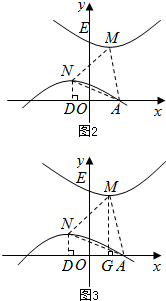
¡àËıßÐÎENFMÊǾØÐΣ»
£¨3£©ÓÉ¡÷AMNΪµÈÑüÈý½ÇÐΣ¬¿É·ÖΪÈçÏÂÈýÖÖÇé¿ö£º
¢ÙÈçͼ2£¬µ±MN=NA=2$\sqrt{2}$ʱ£¬¹ýµãN×÷ND¡ÍxÖᣬ´¹×ãΪµãD£¬ÔòÓÐND=1£¬DA=m-£¨-1£©=m+1£¬
ÔÚRt¡÷NDAÖУ¬NA2=DA2+ND2£¬¼´£¨2$\sqrt{2}$£©2=£¨m+1£©2+12£¬
¡àm1=$\sqrt{7}$-1£¬m2=-$\sqrt{7}$-1£¨²»ºÏÌâÒ⣬ÉáÈ¥£©£¬
¡àA£¨$\sqrt{7}$-1£¬0£©£®
ÓÉÅ×ÎïÏßy=-a£¨x+1£©2+1£¨a£¾0£©µÄ¶Ô³ÆÖáΪx=-1£¬
¡àËüÓëxÖáµÄÁíÒ»¸ö½»µã×ø±êΪ£¨-1-$\sqrt{7}$£¬0£©£®
¡à·½³Ì-a£¨x+1£©2+1=0µÄ½âΪx1=$\sqrt{7}$-1£¬x2=-1-$\sqrt{7}$£®
¢ÚÈçͼ3£¬µ±MA=NAʱ£¬¹ýµãM×÷MG¡ÍxÖᣬ´¹×ãΪG£¬ÔòÓÐOG=1£¬MG=3£¬GA=|m-1|£¬
¡àÔÚRt¡÷MGAÖУ¬MA2=MG2+GA2£¬¼´MA2=32+£¨m-1£©2£¬
ÓÖ¡ßNA2=£¨m+1£©2+12£¬
¡à£¨m+1£©2+12=32+£¨m-1£©2£¬m=2£¬
¡àA£¨2£¬0£©£¬
ÔòÅ×ÎïÏßy=-a£¨x+1£©2+1£¨a£¾0£©µÄ×ó½»µã×ø±êΪ£¨-4£¬0£©£¬
¡à·½³Ì-a£¨x+1£©2+1=0µÄ½âΪx1=2£¬x2=-4£®
¢Ûµ±MN=MAʱ£¬32+£¨m-1£©2=£¨2$\sqrt{2}$£©2£¬
¡àmÎÞʵÊý½â£¬ÉáÈ¥£®
×ÛÉÏËùÊö£¬µ±¡÷AMNΪµÈÑüÈý½ÇÐÎʱ£¬·½³Ì-a£¨x+1£©2=0µÄ½âΪ
x1=$\sqrt{7}$-1£¬x2=-1-$\sqrt{7}$»òx1=2£¬x2=-4£®
µãÆÀ ±¾ÌâÊǶþ´Îº¯ÊýµÄ×ÛºÏÌ⣬¿¼²éÁ˶þ´Îº¯ÊýµÄÐÔÖÊ£¬Èý½ÇÐÎÈ«µÈµÄÅж¨ºÍÐÔÖÊ£¬Æ½ÐÐËıßÐεÄÅж¨£¬´ý¶¨ÏµÊý·¨ÇóÒ»´Îº¯ÊýµÄ½âÎöʽµÈ£¬ÇóµÃAµÄ×ø±êÊǽâÌâµÄ¹Ø¼ü£®


 ÔĶÁ¿ì³µÏµÁдð°¸
ÔĶÁ¿ì³µÏµÁдð°¸
| Ä꼶 | ¸ßÖÐ¿Î³Ì | Ä꼶 | ³õÖÐ¿Î³Ì |
| ¸ßÒ» | ¸ßÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ | ³õÒ» | ³õÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ß¶þ | ¸ß¶þÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õ¶þ | ³õ¶þÃâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ßÈý | ¸ßÈýÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õÈý | ³õÈýÃâ·Ñ¿Î³ÌÍƼö£¡ |
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ

²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
 Èçͼ£¬ÔÚÁâÐÎABCDÖУ¬AB=2£¬¡ÏABC=60¡ã£¬¶Ô½ÇÏßAC¡¢BDÏཻÓÚµãO£¬½«¶Ô½ÇÏßACËùÔÚµÄÖ±ÏßÈƵãO˳ʱÕëÐýת½Ç¦Á£¨0¡ã£¼¦Á£¼90¡ã£©ºóµÃÖ±Ïßl£¬Ö±ÏßlÓëAD¡¢BCÁ½±ß·Ö±ðÏཻÓÚµãEºÍµãF£®
Èçͼ£¬ÔÚÁâÐÎABCDÖУ¬AB=2£¬¡ÏABC=60¡ã£¬¶Ô½ÇÏßAC¡¢BDÏཻÓÚµãO£¬½«¶Ô½ÇÏßACËùÔÚµÄÖ±ÏßÈƵãO˳ʱÕëÐýת½Ç¦Á£¨0¡ã£¼¦Á£¼90¡ã£©ºóµÃÖ±Ïßl£¬Ö±ÏßlÓëAD¡¢BCÁ½±ß·Ö±ðÏཻÓÚµãEºÍµãF£®²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÑ¡ÔñÌâ
| A£® | ÂòÒ»ÕŲÊƱ²»¿ÉÄÜÖн± | B£® | Ã÷Ìì»áÏÂÓê | ||
| C£® | ´ò¿ªµçÊÓÕýÔÚ²¥¹ã¸æ | D£® | ¶ÈÁ¿Èý½ÇÐεÄÄڽǺͽá¹ûÊÇ360¡ã |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÌî¿ÕÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
 Èçͼ£¬Õý·½ÐÎABCDÖУ¬µãE£¬F·Ö±ðÔÚ±ßAB£¬BCÉÏ£¬AF=DE£¬AFºÍDEÏཻÓÚµãG£¬
Èçͼ£¬Õý·½ÐÎABCDÖУ¬µãE£¬F·Ö±ðÔÚ±ßAB£¬BCÉÏ£¬AF=DE£¬AFºÍDEÏཻÓÚµãG£¬²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
 Èçͼ£¬½«¾ØÐÎֽƬABCDÑضԽÇÏßBDÕÛµþ£¬Ê¹µãAÂäÔÚƽÃæÉϵÄFµã´¦£¬DF½»BCÓÚµãE£®
Èçͼ£¬½«¾ØÐÎֽƬABCDÑضԽÇÏßBDÕÛµþ£¬Ê¹µãAÂäÔÚƽÃæÉϵÄFµã´¦£¬DF½»BCÓÚµãE£®²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
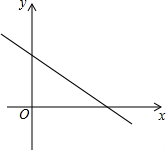 Èçͼ£¬Ö±Ïßl¾¹ýµãA£¨4£¬0£©£¬B£¨0£¬3£©£®
Èçͼ£¬Ö±Ïßl¾¹ýµãA£¨4£¬0£©£¬B£¨0£¬3£©£®²é¿´´ð°¸ºÍ½âÎö>>
¹ú¼ÊѧУÓÅÑ¡ - Á·Ï°²áÁбí - ÊÔÌâÁбí
ºþ±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨Æ½Ì¨ | ÍøÉÏÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | µçÐÅթƾٱ¨×¨Çø | ÉæÀúÊ·ÐéÎÞÖ÷ÒåÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com