

���� ��1����A��-3��0�����Գ���Ϊx=$\frac{5}{2}$��B��0��4���÷����飬��⼴�ɣ�
��2���ı���ABCD�����Σ��������D��C�����꣬��֪A��B���������ֱ�Ϊ��-3��0������0��4��������߶�AB��BC��AD�ij�������AD=BC��AD��BC�����ı���ABCD��ƽ���ı��Σ���AB=BC�������ı���ABCD�����Σ�
��3�������BD��AC�����������ʵ�BD��AC��BM=DM=$\frac{1}{2}$BD=$\sqrt{5}$����AE=t��CF=t����AF=$4\sqrt{5}$-t������E��EH��AC�ڵ�H����֤��AEH�ס�ADM���б���ʽ���EH������S��BEF=S����ABCD-S��AEB-S��BFC-S�ı���EDCF���г�S��t�ĺ�����ϵʽ��
��� �⣺��1�������⣬��$\left\{\begin{array}{l}c=4\\-\frac{b}{{2��\frac{2}{3}}}\end{array}\right.=\frac{5}{2}$�����$\left\{\begin{array}{l}c=4\\ b=-\frac{10}{3}\end{array}\right.$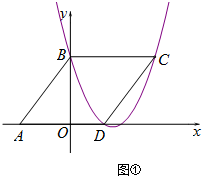
�������ߵĽ���ʽΪ$y=\frac{2}{3}{x^2}-\frac{10}{3}x+4$��
��2���ı���ABCD�����Σ���ͼ�٣�
���ɣ��ߵ�y=0ʱ��$\frac{2}{3}{x^2}-\frac{10}{3}x+4=0$����ã�x1=-3��x2=2��
���D��2��0����
�ߵ�y=4ʱ��$\frac{2}{3}{x^2}-\frac{10}{3}x+4=4$����ã�x1=0��x2=5��
���C��5��4�������������������������� ��
��A��B���������ֱ�Ϊ��-3��0������0��4����
��BC=AD=5��
��BC��AD��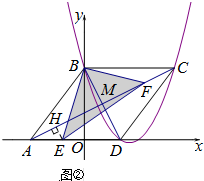
���ı���ABCD��ƽ���ı��Σ�
��Rt��AOB�У���AOB=90�㣬
��AB=$\sqrt{{3^2}+{4^2}}$=5��
��AB=AD��
��?ABCD������
��3����ͼ�ڣ�
�ɵ�B��0��4������D��2��0�����ɵ�BD=$2\sqrt{5}$��
�ɵ�A��-3��0������C��5��4�����ɵ�AC=$4\sqrt{5}$��
������ABCD��
BD��AC��BM=DM=$\frac{1}{2}$BD=$\sqrt{5}$��
�����⣬֪AE=t��CF=t��AF=$4\sqrt{5}$-t��
����E��EH��AC�ڵ�H��
��EH��BD��
���AEH�ס�ADM��
��$\frac{EH}{DM}=\frac{AE}{AD}$������$\frac{EH}{{\sqrt{5}}}=\frac{t}{5}$��
���$EH=\frac{{\sqrt{5}}}{5}t$��
��S��BEF=S����ABCD-S��AEB-S��BFC-S�ı���EDCF
=S����ABCD-S��AEB-S��BFC-��S��ADC-S��AEF��
=$5��4-\frac{1}{2}��4t-\frac{1}{2}��\sqrt{5}t-[{\frac{1}{2}��4\sqrt{5}��\sqrt{5}-\frac{1}{2}����{4\sqrt{5}-t}����\frac{{\sqrt{5}}}{5}t}]$
=$-\frac{{\sqrt{5}}}{10}{t^2}-\frac{{\sqrt{5}}}{2}t+10$��
��S��t�ĺ�����ϵʽΪ��S=$-\frac{{\sqrt{5}}}{10}{t^2}-\frac{{\sqrt{5}}}{2}t+10$��
���� ������Ҫ�����˴���ϵ���������ʽ�����ε��ж������ʡ����������ε��ж������ʡ����ɶ����Լ���������к�������ʽ�������ۺ��Խ�ǿ����һ���Ѷȣ�����С�����ѵ㣬�ؼ����ҵ���BEF����ķֽⷽ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
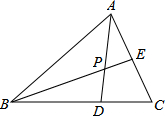 ��ͼ����ABC�����Ϊ3��BD��DC=2��1��E��AC���е㣬AD��BE�ཻ�ڵ�P����ô�ı���PDCE�����Ϊ��������
��ͼ����ABC�����Ϊ3��BD��DC=2��1��E��AC���е㣬AD��BE�ཻ�ڵ�P����ô�ı���PDCE�����Ϊ��������| A�� | $\frac{1}{3}$ | B�� | $\frac{7}{10}$ | C�� | $\frac{3}{5}$ | D�� | $\frac{13}{20}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
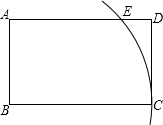 ��ͼ���ھ���ABCD�У�$\frac{AB}{BC}=\frac{3}{5}$���Ե�BΪԲ�ģ�BC��Ϊ�뾶����������AD�ڵ�E����AE•ED=8�������ABCD�����Ϊ30��
��ͼ���ھ���ABCD�У�$\frac{AB}{BC}=\frac{3}{5}$���Ե�BΪԲ�ģ�BC��Ϊ�뾶����������AD�ڵ�E����AE•ED=8�������ABCD�����Ϊ30���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
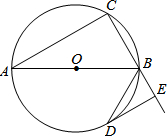 ��֪����ͼ��AB�ǡ�O��ֱ������C�ڡ�O�ϣ���ABC�����ƽ����BD����O�ڵ�D��DE��CB���ӳ����ڵ�E��
��֪����ͼ��AB�ǡ�O��ֱ������C�ڡ�O�ϣ���ABC�����ƽ����BD����O�ڵ�D��DE��CB���ӳ����ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����?ABCD�У��Խ���AC��BD�ཻ�ɵ���Ǧ�Ϊ60�㣬��AC=10��BD=8����?ABCD�������20$\sqrt{3}$��
��ͼ����?ABCD�У��Խ���AC��BD�ཻ�ɵ���Ǧ�Ϊ60�㣬��AC=10��BD=8����?ABCD�������20$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪���κ���L1��y=ax2-2ax+a+3��a��0���Ͷ��κ���L2��y=-a��x+1��2+1��a��0��ͼ��Ķ���ֱ�ΪM��N����y��ֱ��ڵ�E��F��
��ͼ����֪���κ���L1��y=ax2-2ax+a+3��a��0���Ͷ��κ���L2��y=-a��x+1��2+1��a��0��ͼ��Ķ���ֱ�ΪM��N����y��ֱ��ڵ�E��F���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com