
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
分析 根据进入决赛的15名学生所得分数互不相同,所以这15名学生所得分数的中位数即是获奖的学生中的最低分,所以某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是中位数,据此解答即可.
解答 解:∵进入决赛的15名学生所得分数互不相同,(15+1)÷2=8,
∴这15名学生所得分数的中位数即是获奖的学生中的最低分,
∴某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是中位数,
如果这名学生的分数大于或等于中位数,则他能获奖,
如果这名学生的分数小于中位数,则他不能获奖.
故选:B.
点评 此题主要考查了统计量的选择,要熟练掌握,解答此题的关键是要明确:①数据的平均数、众数、中位数是描述一组数据集中趋势的特征量,极差、方差是衡量一组数据偏离其平均数的大小(即波动大小)的特征数,描述了数据的离散程度.②极差和方差的不同点:极差表示一组数据波动范围的大小,一组数据极差越大,则它的波动范围越大;方差和标准差反映了一组数据与其平均值的离散程度的大小.方差(或标准差)越大,数据的历算程度越大,稳定性越小;反之,则离散程度越小,稳定性越好.


科目:初中数学 来源: 题型:解答题
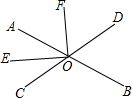 如图,O是直线AB上一点,过O作射线OE、OF.OE平分∠AOC,∠AOC=∠BOD.
如图,O是直线AB上一点,过O作射线OE、OF.OE平分∠AOC,∠AOC=∠BOD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
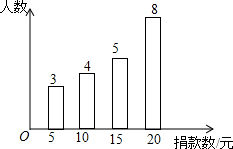 某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,根据这组数据绘制成如图所示的统计图.
某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,根据这组数据绘制成如图所示的统计图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
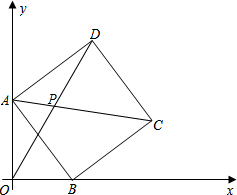 如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,AC,OD交于点P,其中OA=4,OB=3.
如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,AC,OD交于点P,其中OA=4,OB=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com