
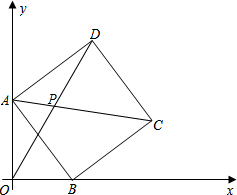
 如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,AC,OD交于点P,其中OA=4,OB=3.
如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,AC,OD交于点P,其中OA=4,OB=3.分析 (1)根据正方形的性质,可得AD与AB的关系,∠DAB的度数,根据余角的性质,可得∠DAE=∠ABO,根据全等三角形的判定与性质,可得AE、DE的长度,根据待定系数法,可得答案;
(2)根据全等三角形的判定与性质,可得BF、CF的长度,根据待定系数法,可得CA的解析式,根据解方程组,可得P点坐标,根据三角形的面积公式,可得答案.
解答 解:(1)过点D作DE⊥OA于点E,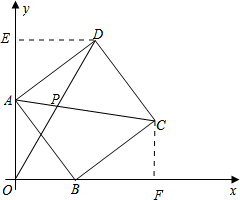 ,
,
∵四边形ABCD是正方形
∴AD=AB,∠DAB=∠DEA=∠DAB=90°.
∵OA⊥OB
∴∠DAE+∠OAB=∠OAB+∠ABO=90°
∴∠DAE=∠ABO
在DAE和AOB中,
$\left\{\begin{array}{l}{∠DEA=∠AOB}\\{∠DAE=∠ABO}\\{DA=AB}\end{array}\right.$,
∴△DEA≌△AOB (AAS)
∴DE=AO=4,AE=BO=3
∴OE=AE+AO=3+4=7
∴点D的坐标为(4,7).
设OD所在直线的解析式为y=k1x (k1≠0)
将点D (4,7)代入得:4k1=7,
解得:k1=$\frac{7}{4}$,
所以OD所在直线的解析式为y=$\frac{7}{4}$x;
(2)过点C作CF⊥OB于点F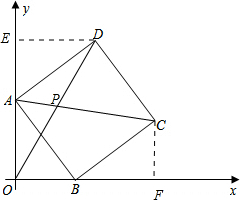 ,
,
由第(1)问易得:△AOB≌BFC,
BF=4,CF=3,
∴OF=OB+BF=7,
∴点A的坐标为(0,4),点C的坐标为(7,3)
设AC所在直线的解析式为y=2x+b (k2≠0),
将点A(0,4),点C(7,3)代入得:$\left\{\begin{array}{l}{b=4}\\{7{k}_{2}+b=3}\end{array}\right.$
解得:$\left\{\begin{array}{l}{{k}_{2}=-\frac{1}{7}}\\{b=4}\end{array}\right.$,所以AC所在直线的解析式为y=-$\frac{1}{7}$x+4,
联立OD、AC得方程组$\left\{\begin{array}{l}{y=\frac{7}{4}x}\\{y=-\frac{1}{7}x+4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=\frac{112}{53}}\\{y=\frac{196}{53}}\end{array}\right.$
∴点P的坐标为($\frac{112}{53}$,$\frac{196}{53}$)
∴S△OAP=$\frac{1}{2}$OA•xP$\frac{1}{2}$×4×$\frac{112}{53}$=$\frac{224}{53}$.
点评 本题考查了一次函数综合题,(1)利用了正方形的性质,余角的性质,全等三角形的判定与性质,待定系数法求函数解析式;(2)利用了全等三角形的判定与性质,待定系数法求函数解析式,解方程组求交点坐标,三角形的面积公式.


科目:初中数学 来源: 题型:解答题
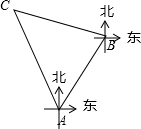 某航班在某日凌晨0:40从甲地(记为A)起飞,沿北偏东35°方向出发,以870km/h的速度直线飞往乙地,但飞机在当日凌晨1:20左右在B处突然改变航向,沿北偏西71°方向飞到C处消失,如果此航班在C处发出求救信号,又测得C在A的北偏西25°方向,求A与求救点C的距离(结果保留整数,参考数据:sin74°≈$\frac{24}{25}$,sin46°≈$\frac{18}{25}$).
某航班在某日凌晨0:40从甲地(记为A)起飞,沿北偏东35°方向出发,以870km/h的速度直线飞往乙地,但飞机在当日凌晨1:20左右在B处突然改变航向,沿北偏西71°方向飞到C处消失,如果此航班在C处发出求救信号,又测得C在A的北偏西25°方向,求A与求救点C的距离(结果保留整数,参考数据:sin74°≈$\frac{24}{25}$,sin46°≈$\frac{18}{25}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
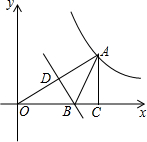 如图,点A在双曲线y=$\frac{3}{x}$(x>0)上,过点A作AC⊥x轴,垂足为C,线段OA的垂直平分线BD交x轴于点B,△ABC的周长为4,求点A的坐标.
如图,点A在双曲线y=$\frac{3}{x}$(x>0)上,过点A作AC⊥x轴,垂足为C,线段OA的垂直平分线BD交x轴于点B,△ABC的周长为4,求点A的坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com