

���� ��1�����ô���ϵ�������A��B��D�����꣬�ɡ�BOD�ա�BOE���Ƴ�OD=OE���Ƴ�E��0��-5������ֱ��BE�Ľ���ʽΪy=kx+b������$\left\{\begin{array}{l}{b=-5}\\{10k+b=0}\end{array}\right.$���ⷽ���鼴�ɽ�����⣮
��2����ͼ1�У�����A����ֱ��BE�ĶԳƵ�A�䣬����AA�佻BE��K����A��N��AB��N��BE��M����ʱAM+MN��ֵ��С����취���ߵ�A�����꼴�ɽ�����⣮
��3���������������ۼ��ɢٵ���FK����RG��ͬһֱ����ʱ���ڵ���QK����RJ��ͬһֱ����ʱ���۵���FQ����JG��ͬһֱ����ʱ���ֱ��г����̼��ɽ�����⣮
��� �⣺��1������������y=-$\frac{1}{2}$x2+$\frac{9}{2}$x+5����x=0��y=5����y=0��-$\frac{1}{2}$x2+$\frac{9}{2}$x+5=0���x=-1��10��
��D��0��5����A��-1��0����B��10��0����
�ڡ�BOD�͡�BOE�У�
$\left\{\begin{array}{l}{��DBO=��EBO}\\{BO=BO}\\{��BOD=��BOE}\end{array}\right.$��
���BOD�ա�BOE��
��OD=OE��
��E��0��-5����
��ֱ��BE�Ľ���ʽΪy=kx+b������$\left\{\begin{array}{l}{b=-5}\\{10k+b=0}\end{array}\right.$�����$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-5}\end{array}\right.$��
��ֱ��BE�Ľ���ʽΪy=$\frac{1}{2}$x-5��
��2����ͼ1�У�����A����ֱ��BE�ĶԳƵ�A�䣬����AA�佻BE��K����A��N��AB��N��BE��M����ʱAM+MN��ֵ��С��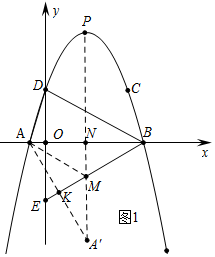
��ֱ��AA��Ľ���ʽΪy=-2x-2��
��$\left\{\begin{array}{l}{y=-2x-2}\\{y=\frac{1}{2}x-5}\end{array}\right.$���$\left\{\begin{array}{l}{x=\frac{6}{5}}\\{y=-\frac{22}{5}}\end{array}\right.$��
��K��$\frac{6}{5}$��-$\frac{22}{5}$����
��AK=KA�䣬
��A�䣨$\frac{17}{5}$��-$\frac{44}{5}$����
��M��$\frac{17}{5}$��-$\frac{33}{10}$����
��x=$\frac{17}{5}$ʱ��Py=-$\frac{1}{2}$��$\frac{17}{5}$��2+$\frac{9}{2}$��$\frac{17}{5}$+5=$\frac{363}{25}$��
���P������$\frac{17}{5}$��$\frac{363}{25}$����
��3����ͼ2�У��ӳ�FK��x����E���ӳ�JR��x����P��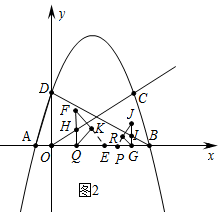
��C��9��5����
��ֱ��OC�Ľ���ʽΪy=$\frac{5}{9}$x��
��OQ=t��BG=2t��
��HQ=$\frac{5}{9}$t��IG=t��
�ߡ�FKQ����RJG�ǵ���ֱ�������Σ�
���F=��FEQ=45�㣬
��QE=QF=$\frac{10}{9}$t��PG=JG=2t��
�ٵ���FK����RG��ͬһֱ����ʱ��t+$\frac{10}{9}$t+2t=10�����t=$\frac{90}{37}$��
�ڵ���QK����RJ��ͬһֱ����ʱ��t+4t=10�����t=2��
�۵���FQ����JG��ͬһֱ����ʱ��t+2t=10�����t=$\frac{10}{3}$��
��������������Q�˶�$\frac{90}{37}$���2���$\frac{10}{3}$��ʱ����������ֱ�������ηֱ���һ��ǡ������ͬһֱ���ϣ�
���� ���⿼����κ����ۺ��⡢һ�κ�����Ӧ�á�����ֱ�������ε����ʡ����߶���̡�һԪһ�η��̵�֪ʶ������Ĺؼ������������ѧ֪ʶ��ѧ�ṹ��һ�κ��������÷�����������ֱ�ߵĽ������꣬ѧ���÷������۵�˼��˼�����⣬ѧ�ṹ�����̽�����⣬�����п�ѹ���⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��-3 | B�� | x��-3 | C�� | x��-3 | D�� | x=-3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���� | B�� | ������ | C�� | ���� | D�� | �Ǹ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���ж���ͼ����x���Ƿ��н��� | |
| B�� | ��Գ�����x�ύ�ڸ����� | |
| C�� | ���㣨m��n����y=x2-bx-1��ͼ���ϣ���n��-1 | |
| D�� | ���㣨-3��y1������2��y2������y=x2-bx-1��ͼ���ϣ���y1��y2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| x | 0 | 2 | 3 |
| y | 0.37 | 0.37 | 4 |
| A�� | 20 | B�� | 8 | C�� | 24 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
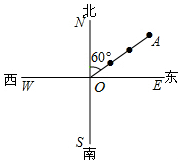 ��ͼ������O�ں��й����У������ı�ƫ��60�㷽���ϣ���֮���30���ﴦ���ֵ���A��ͬʱ��������ƫ��30�㷽���ϣ���֮���20���ﴦ���ֻ���B�����������Ϸ����Ϸ��ֿ���C��������Ҫ����
��ͼ������O�ں��й����У������ı�ƫ��60�㷽���ϣ���֮���30���ﴦ���ֵ���A��ͬʱ��������ƫ��30�㷽���ϣ���֮���20���ﴦ���ֻ���B�����������Ϸ����Ϸ��ֿ���C��������Ҫ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��AD�ǡ�ABC�Ľ�ƽ���ߣ�DE��DF�ֱ��ǡ�ABD�͡�ACD�ĸߣ�������˵����ȷ���ǣ�������
��ͼ��AD�ǡ�ABC�Ľ�ƽ���ߣ�DE��DF�ֱ��ǡ�ABD�͡�ACD�ĸߣ�������˵����ȷ���ǣ�������| A�� | AD��ֱFE | B�� | ADƽ��EF | C�� | EF��ֱƽ��AD | D�� | AD��ֱƽ��EF |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=ax+b��ͼ���뷴��������y=$\frac{k}{x}$��ͼ���ཻ�ڵ�A��-4��-2����B��m��4������y���ཻ�ڵ�C��
��ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=ax+b��ͼ���뷴��������y=$\frac{k}{x}$��ͼ���ཻ�ڵ�A��-4��-2����B��m��4������y���ཻ�ڵ�C���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com