Question

【题目】操作与证明：

如图1，把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点C重合，点E、F分别在正方形的边CB、CD上，连接AF．取AF中点M，EF的中点N，连接MD、MN．

（1）连接AE，求证：△AEF是等腰三角形；

猜想与发现：

（2）在（1）的条件下，请判断线段MD与MN的关系，得出结论；

结论：DM、MN的关系是：　 　；

拓展与探究：

（3）如图2，将图1中的直角三角板ECF绕点C旋转180°，其他条件不变，则（2）中的结论还成立吗？若成立，请加以证明；若不成立，请说明理由．

Answer 1

【答案】（1）证明见解析；（2）DM＝MN，DM⊥MN；（3）成立，理由见解析.

【解析】

（1）先证明△ABE≌△ADF，再利用全等三角形的性质即可证明△AEF是等腰三角形；

（2）利用三角形中位线定理，直角三角形斜边中线定理可证明DM=MN，再证明∠DMN=∠DAB=90°，即可解决问题；

（3）连接AE，交DM于O，交CD于G，同（2）证明方法类似，可证明DM=MN，再证明∠DOG＝∠ECG＝90°，即可得出结论.

（1）证明：如图，

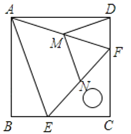
∵四边形ABCD是正方形，

∴AB＝BC＝CD＝AD，∠B＝∠ADF＝90°，

∵△EFC是等腰直角三角形，

∴CE＝CF，

∴BE＝DF，

∴△ABE≌△ADF，

∴AE＝AF，

∴△AEF是等腰三角形；

（2）解：结论：DM＝MN，DM⊥MN，

证明：∵在Rt△ADF中， M是AF的中点，

∴DM=AF，

∵M是AF的中点，N是EF的中点，

∴MN=AE，MN∥AE，

∵AE＝AF，

∴MN＝DM，

∵∠ADF＝90°，AM＝MF，

∴MD＝MA＝MF，

∴∠MAD＝∠ADM，

∴∠DMF＝∠MAD+∠ADM＝2∠DAM，

∵△ABE≌△ADF，

∴∠BAE＝∠DAF，

∴∠DAB=∠EAF+2∠DAM＝90°，

∵MN∥AE，

∴∠NMF＝∠EAF，

∴∠DMN=∠NMF+∠DMF＝∠EAF+2∠DAM＝∠DAB=90°，

∴DM⊥MN，

∴MN＝DM，MN⊥DM，

故答案为MN＝DM，MN⊥DM；

（3）解：结论仍然成立．

理由：如图，连接AE，设AE交DM于O，交CD于G，

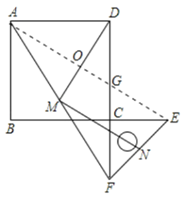
∵四边形ABCD是正方形，

∴AB＝BC＝CD＝AD，∠B＝∠ADF＝90°，

又∵BC+CE=CD+CF,即BE＝DF，

∴△ABE≌△ADF，

∴AF＝AE，∠AFD＝∠AEB，

∵在Rt△ADF中，M是AF的中点，

∴DM=AF，

∵M是AF的中点，N是EF的中点，

∴MN=AE，MN∥AE，

∴MN＝DM，

∵∠ADF＝90°，AM＝MF，

∴MD＝MA＝MF，

∴∠MDF＝∠MFD＝∠AEB，

∵∠DGO＝∠CGE，∠ODG＝∠CEG，

∴∠DOG＝∠ECG＝90°，

∵NM∥AE，

∴∠DOG＝∠DMN＝90°，

∴MN⊥DM，MN＝DM．