练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．$\sqrt{25}$的平方根是$±\sqrt{5}$，1.44的算术平方根是1.2．

    分析 根据平方运算，可得平方根、算术平方根．

    解答 解：$\sqrt{25}$的平方根是±$\sqrt{5}$，1.44的算术平方根是1.2；
    故答案为：$±\sqrt{5}$；1.2．

    点评 本题考查了算术平方根，平方运算是求平方根的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

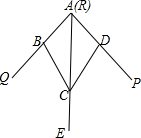    6．如图，小敏做了一个角平分仪ABCD，其中AB=AD，BC=DC．将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线．此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE=∠PAE．则说明这两个三角形全等的依据是（　　）
    A．SASB．ASAC．AASD．SSS

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．三角形三边长为6、8、10，那么最长边上的高为（　　）
    A．6B．4.5C．4.8D．8

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．已知a=2-$\sqrt{3}$，b=$\sqrt{3}+2$，则a、b的关系为（　　）
    A．相等B．互为相反数C．互为倒数D．互为负倒数

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．仔细算一算，要细心哦：
    （1）$-\sqrt{1\frac{99}{225}}$
    （2）$\frac{1}{2}\sqrt{0.25}+\frac{1}{3}\sqrt{0.36}$
    （3）$\root{3}{{3\frac{3}{8}}}$
    （4）$-\root{3}{-1000}$
    （5）$±\sqrt{1\frac{13}{36}}$
    （6）$\root{3}{-8}+\sqrt{16}$
    （7）-4×$\root{3}{{-15\frac{5}{8}}}$
    （8）$\sqrt{{{（{±\frac{2}{3}}）}^2}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．某居民生活小区需要建一个大型的球形储水罐，需储水13.5立方米，那么这个球罐的半径r为多少米（球的体积V=$\frac{4}{3}π{r^3}$，π取3.14，结果精确到0.1米）？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．若二项式9m2+1加上一个含m的单项式后是一个关于m的完全平方式，则符合要求的单项式的个数有（　　）
    A．4个B．3个C．2个D．1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

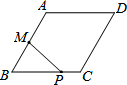    10．如图，菱形ABCD中，AB=2，∠B=60°，M为AB的中点．动点P在菱形的边上从点B出发，沿B→C→D的方向运动，到达点D时停止．连接MP，设点P运动的路程为x，MP 2=y，则表示y与x的函数关系的图象大致为（　　）
    A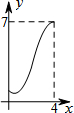．B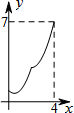．C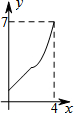．D．?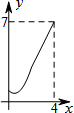

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

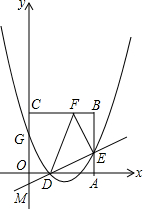    11．如图所示，正方形OABC的边长为2cm，以OA、OC所在直线为坐标轴建立直角坐标系xoy，点D、E、F和G分别从点O、A、B和C沿着OA、AB、BC和CO方向都以1cm/s的速度同时移动，移动时间为t（0＜t＜2）s，抛物线y=ax2+bx+c总是经过三个动点G、D、E．
    （1）判断△DEF的形状，并说明理由；
    （2）△DEF的面积是否存在最大值或最小值？若存在，请求出最大值或最小值以及相应的点坐标．若不存在请说明理由；
    （3）设直线DE与y轴交于点M．当ME=3MD时，请求出抛物线的解析式；
    （4）图中的抛物线是动点移动到某一时刻的图象，此时抛物线上是否存在点P，使过点P的直线l平分正方形的面积，且点D和点E到直线l的距离相等？若存在，请在图中画出l和抛物线的所有交点；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案