
【题目】已知y+1与x+2成正比例,且当x=4时,y=-4.
(1)求y关于x的函数关系式;
(2)若点(a,2)和(2,b)均在(1)中函数图像上,求a、b的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
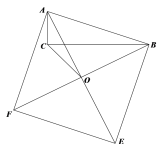
【题目】如图,以Rt![]() 的斜边AB为一边在
的斜边AB为一边在![]() 同侧作正方形ABEF.点O为AE与BF的交点,连接CO,若CA = 2,
同侧作正方形ABEF.点O为AE与BF的交点,连接CO,若CA = 2,![]() ,那么四边形ABOC的面积为_______.
,那么四边形ABOC的面积为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
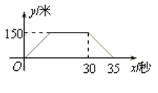
【题目】火车匀速通过隧道时,火车在隧道内的长度![]() (米)与火车行驶时间
(米)与火车行驶时间![]() (秒)之间的关系用图象描述如图所示,有下列结论:
(秒)之间的关系用图象描述如图所示,有下列结论:
①火车的长度为120米;
②火车的速度为30米/秒;
③火车整体都在隧道内的时间为25秒;
④隧道长度为750米.
其中正确的结论是_____.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
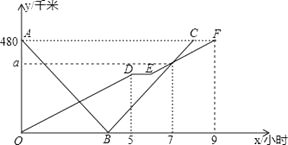
【题目】(本题满分12分)快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速继续向甲地行驶,到达甲地后停止行驶;快车到达乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程![]() (千米)与所用时间
(千米)与所用时间![]() (小时)之间的函数图象如图,请结合图象信息解答下列问题:
(小时)之间的函数图象如图,请结合图象信息解答下列问题:
(1)求慢车的行驶速度和![]() 的值;
的值;
(2)求快车与慢车第一次相遇时,距离甲地的路程是多少千米?
(3)求两车出发后几小时相距的路程为![]() 千米?
千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
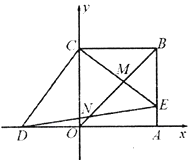
【题目】如图,在平面直角坐标系中,正方形![]() 两顶点为
两顶点为![]() ,
,![]() ,点D的坐标为
,点D的坐标为![]() ,在
,在![]() 上取点E,使得
上取点E,使得![]() ,连接
,连接![]() ,分别交
,分别交![]() ,
,![]() 于M,N两点.
于M,N两点.
(1)求证:![]() ;
;
(2)求点E的坐标和线段![]() 所在直线的解析式;
所在直线的解析式;
(3)在M,N两点中任选一点求出它的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.

(1)求A,B两种品牌的足球的单价.
(2)求该校购买20个A品牌的足球和2个B品牌的足球的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA的方向是北偏东15°,OB的方向是西偏北50°,OD是OB的反向延长线.

(1)若∠AOC=∠AOB,求OC的方向.
(2)在(1)问的条件下,作∠AOD的角平分线OE,求∠COE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】节约是中华民族的传统美德.为倡导市民节约用水的意识,某市对市民用水实行“阶梯收费”,制定了如下用水收费标准:每户每月的用水不超过![]() 立方米时,水价为每立方米
立方米时,水价为每立方米![]() 元,超过
元,超过![]() 立方米时,超过的部分按每立方米
立方米时,超过的部分按每立方米![]() 元收费.
元收费.
(1)该市某户居民9月份用水![]() 立方米(
立方米(![]() ),应交水费
),应交水费![]() 元,请你用含
元,请你用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)如果某户居民12月份交水费![]() 元,那么这个月该户居民用了多少立方米水?
元,那么这个月该户居民用了多少立方米水?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com