
ЎҫМвДҝЎҝҪЪФјКЗЦР»ӘГсЧеөДҙ«НіГАөВ.ОӘі«өјКРГсҪЪФјУГЛ®өДТвК¶,ДіКР¶ФКРГсУГЛ®КөРРЎ°ҪЧМЭКХ·СЎұЈ¬ЦЖ¶ЁБЛИзПВУГЛ®КХ·СұкЧј:Гҝ»§ГҝФВөДУГЛ®І»і¬№э![]() Бў·ҪГЧКұЈ¬Л®јЫОӘГҝБў·ҪГЧ
Бў·ҪГЧКұЈ¬Л®јЫОӘГҝБў·ҪГЧ![]() ФӘ,і¬№э
ФӘ,і¬№э![]() Бў·ҪГЧКұЈ¬і¬№эөДІҝ·Ц°ҙГҝБў·ҪГЧ
Бў·ҪГЧКұЈ¬і¬№эөДІҝ·Ц°ҙГҝБў·ҪГЧ![]() ФӘКХ·С.
ФӘКХ·С.
(1)ёГКРДі»§ҫУГс9ФВ·ЭУГЛ®![]() Бў·ҪГЧ(
Бў·ҪГЧ(![]() )Ј¬УҰҪ»Л®·С
)Ј¬УҰҪ»Л®·С![]() ФӘЈ¬ЗлДгУГә¬
ФӘЈ¬ЗлДгУГә¬![]() өДҙъКэКҪұнКҫ
өДҙъКэКҪұнКҫ![]() ;
;
(2)Из№ыДі»§ҫУГс12ФВ·ЭҪ»Л®·С![]() ФӘ,ДЗГҙХвёцФВёГ»§ҫУГсУГБЛ¶аЙЩБў·ҪГЧЛ®?
ФӘ,ДЗГҙХвёцФВёГ»§ҫУГсУГБЛ¶аЙЩБў·ҪГЧЛ®?
Ўҫҙр°ёЎҝ(1) y=2.5x-10ЈЁ![]() Ј©Ј»(2) 14
Ј©Ј»(2) 14
ЎҫҪвОцЎҝ
(1)ёщҫЭУГЛ®КХ·СұкЧјЈ¬јҙҝЙөГөҪә¬![]() өДҙъКэКҪұнКҫ
өДҙъКэКҪұнКҫ![]() Ј»
Ј»
(2)°Сy=25Ј¬ҙъИлy=2.5x-10Ј¬јҙҝЙөГөҪҙр°ё.
(1)ёщҫЭМвТвөГЈәy=10ЎБ1.5+2.5(x-10)Ј¬
јҙЈәy=2.5x-10ЈЁ![]() Ј©Ј»
Ј©Ј»
(2)ЎЯ25>10ЎБ1.5Ј¬
ЎаДі»§ҫУГс12ФВ·ЭөДУГЛ®Бҝі¬№э10Бў·ҪГЧЈ¬
өұy=25КұЈ¬25=2.5x-10Ј¬ҪвөГЈәx=14Ј¬
ҙрЈәХвёцФВёГ»§ҫУГсУГБЛ14Бў·ҪГЧЛ®.


 И«УЕҝјөдөҘФӘјмІвҫнј°№йАаЧЬёҙП°ПөБРҙр°ё
И«УЕҝјөдөҘФӘјмІвҫнј°№йАаЧЬёҙП°ПөБРҙр°ё Ж·С§Л«УЕҫнПөБРҙр°ё
Ж·С§Л«УЕҫнПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘy+1Улx+2іЙХэұИАэЈ¬ЗТөұx=4КұЈ¬y=Јӯ4Ј®
(1)Зуy№ШУЪxөДәҜКэ№ШПөКҪЈ»
(2)Ифөг(aЈ¬2)әН(2Ј¬b)ҫщФЪ(1)ЦРәҜКэНјПсЙПЈ¬ЗуaЎўbөДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
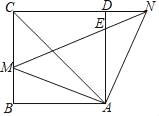
ЎҫМвДҝЎҝИзНјЈ¬ФЪХэ·ҪРОABCDЦРЈ¬өгMКЗұЯBCЙПөДТ»өгЈЁІ»УлBЎўCЦШәПЈ©Ј¬өгNФЪCDұЯөДСУіӨПЯЙПЈ¬ЗТВъЧгЎПMAN=90ЎгЈ¬БӘҪбMNЎўACЈ¬NУлұЯADҪ»УЪөгEЈ®
ЈЁ1Ј©ЗуЦӨЈәAM=ANЈ»
ЈЁ2Ј©Из№ыЎПCAD=2ЎПNADЈ¬ЗуЦӨЈәAM2=ACAEЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝОӘҙтФмГААцРЈФ°Ј¬РЎГчЎўРЎәмОӘРЈФ°ДЪөДТ»ҝйҝХөШ·ЦұрМṩБЛИзНјјЧЎўТТөДЙијЖ·Ҫ°ёЈ¬ЖдЦРТхУ°Іҝ·Ц¶јУГУЪВМ»ҜЈ¬НјјЧҝХ°ЧЗшУтРЮҪЁТ»ЧщөсПсЈ¬НјТТҝХ°ЧЗшУтРЮҪЁКҜЧУРЎВ·Ј®ТСЦӘSјЧұнКҫНјјЧЦРВМ»ҜөДГж»эSТТұнКҫНјТТЦРВМ»ҜөДГж»эЈ®
ЈЁ1Ј©SјЧЈҪЎЎ ЎЎЈЁУГә¬aЈ¬bөДҙъКэКҪұнКҫЈ©Ј»
ЈЁ2Ј©ЙиkЈҪ![]() Ј¬
Ј¬
ўЩЗлУГә¬aЈ¬bөДҙъКэКҪұнКҫkІў»ҜјтЈ»
ўЪөұ2SјЧ©ҒSТТЈҪ![]() a2КұЈ¬ЗуkөДЦөЈ®
a2КұЈ¬ЗуkөДЦөЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪRtЎчABCЦРЈ¬ЎПC=90ЎгЈ¬ТФACОӘЦұҫ¶ЧчЎСOЈ¬Ҫ»ABУЪDЈ¬№эөгOЧчOEЎОABЈ¬Ҫ»BCУЪEЈ®
ЈЁ1Ј©ЗуЦӨЈәEDОӘЎСOөДЗРПЯЈ»
ЈЁ2Ј©Из№ыЎСOөД°лҫ¶ОӘ![]() Ј¬ED=2Ј¬СУіӨEOҪ»ЎСOУЪFЈ¬Б¬ҪУDFЎўAFЈ¬ЗуЎчADFөДГж»эЈ®
Ј¬ED=2Ј¬СУіӨEOҪ»ЎСOУЪFЈ¬Б¬ҪУDFЎўAFЈ¬ЗуЎчADFөДГж»эЈ®

Ўҫҙр°ёЎҝЈЁ1Ј©ЦӨГчјыҪвОцЈ»ЈЁ2Ј©![]()
ЎҫҪвОцЎҝКФМв·ЦОцЈәЈЁ1Ј©КЧПИБ¬ҪУODЈ¬УЙOEЎОABЈ¬ёщҫЭЖҪРРПЯУлөИСьИэҪЗРОөДРФЦКЈ¬ТЧЦӨөГ![]() ЎХ
ЎХ![]() јҙҝЙөГ
јҙҝЙөГ![]() Ј¬ФтҝЙЦӨөГ
Ј¬ФтҝЙЦӨөГ![]() ОӘ
ОӘ![]() өДЗРПЯЈ»
өДЗРПЯЈ»
ЈЁ2Ј©Б¬ҪУCDЈ¬ёщҫЭЦұҫ¶Лщ¶ФөДФІЦЬҪЗКЗЦұҪЗЈ¬јҙҝЙөГ![]() АыУГ№ҙ№Й¶ЁАнјҙҝЙЗуөГ
АыУГ№ҙ№Й¶ЁАнјҙҝЙЗуөГ![]() өДіӨЈ¬УЦУЙOEЎОABЈ¬ЦӨөГ
өДіӨЈ¬УЦУЙOEЎОABЈ¬ЦӨөГ![]() ёщҫЭПаЛЖИэҪЗРОөД¶ФУҰұЯіЙұИАэЈ¬јҙҝЙЗуөГ
ёщҫЭПаЛЖИэҪЗРОөД¶ФУҰұЯіЙұИАэЈ¬јҙҝЙЗуөГ![]() өДіӨЈ¬И»әуАыУГИэҪЗәҜКэөДЦӘК¶Ј¬ЗуөГ
өДіӨЈ¬И»әуАыУГИэҪЗәҜКэөДЦӘК¶Ј¬ЗуөГ![]() Ул
Ул![]() өДіӨЈ¬И»әуАыУГSЎчADF=SМЭРОABEF-SМЭРОDBEFЗуөГҙр°ёЈ®
өДіӨЈ¬И»әуАыУГSЎчADF=SМЭРОABEF-SМЭРОDBEFЗуөГҙр°ёЈ®
КФМвҪвОцЈә(1)ЦӨГчЈәБ¬ҪУODЈ¬

ЎЯOEЎОABЈ¬
ЎаЎПCOE=ЎПCADЈ¬ЎПEOD=ЎПODAЈ¬
ЎЯOA=OD,
ЎаЎПOAD=ЎПODAЈ¬
ЎаЎПCOE=ЎПDOEЈ¬
ФЪЎчCOEәНЎчDOEЦРЈ¬
 ЎаЎчCOEЎХЎчDOE(SAS)Ј¬
ЎаЎчCOEЎХЎчDOE(SAS)Ј¬
![]()
ЎаEDЎНODЈ¬
ЎаEDКЗ![]() өДЗРПЯЈ»
өДЗРПЯЈ»
(2)Б¬ҪУCDЈ¬Ҫ»OEУЪMЈ¬
ФЪRtЎчODEЦРЈ¬
ЎЯOD=32Ј¬DE=2Ј¬
![]()
ЎЯOEЎОABЈ¬
ЎаЎчCOEЎЧЎчCABЈ¬
![]() ЎаAB=5Ј¬
ЎаAB=5Ј¬
ЎЯACКЗЦұҫ¶Ј¬
![]()
![]()
![]()
![]()
ЎЯEFЎОABЈ¬
![]()
![]()
![]()
ЎаSЎчADF=SМЭРОABEFSМЭРОDBEF
![]()
ЎаЎчADFөДГж»эОӘ![]()

ЎҫМвРНЎҝҪвҙрМв
ЎҫҪбКшЎҝ
25
ЎҫМвДҝЎҝЎҫМвДҝЎҝТСЦӘЈ¬ЕЧОпПЯy=ax2+ax+bЈЁaЎЩ0Ј©УлЦұПЯy=2x+mУРТ»ёц№«№ІөгMЈЁ1Ј¬0Ј©Ј¬ЗТaЈјbЈ®
ЈЁ1Ј©ЗуbУлaөД№ШПөКҪәНЕЧОпПЯөД¶ҘөгDЧшұкЈЁУГaөДҙъКэКҪұнКҫЈ©Ј»
ЈЁ2Ј©ЦұПЯУлЕЧОпПЯөДБнНвТ»ёцҪ»өгјЗОӘNЈ¬ЗуЎчDMNөДГж»эУлaөД№ШПөКҪЈ»
ЈЁ3Ј©a=©Ғ1КұЈ¬ЦұПЯy=©Ғ2xУлЕЧОпПЯФЪөЪ¶юПуПЮҪ»УЪөгGЈ¬өгGЎўH№ШУЪФӯөг¶ФіЖЈ¬ПЦҪ«ПЯ¶ОGHСШyЦбПтЙПЖҪТЖtёцөҘО»ЈЁtЈҫ0Ј©Ј¬ИфПЯ¶ОGHУлЕЧОпПЯУРБҪёцІ»Н¬өД№«№ІөгЈ¬КФЗуtөДИЎЦө·¶О§Ј®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝОКМвМбіцЈә
ДіРЈТӘҫЩ°мЧгЗтИьЈ¬ИфУР5Ц§Зт¶УҪшРРөҘСӯ»·ұИИьЈЁјҙИ«ІҝұИИь№эіМЦРИОәОТ»¶У¶јТӘ·ЦұрУлЖдЛыёч¶УұИИьТ»іЎЗТЦ»ұИИьТ»іЎЈ©Ј¬ФтёГРЈТ»№ІТӘ°ІЕЕ¶аЙЩіЎұИИьЈҝ
№№ҪЁДЈРНЈә
Йъ»оЦРөДРн¶аКөјКОКМвЈ¬НщНщРиТӘ№№ҪЁПаУҰөДКэС§ДЈРНЈ¬АыУГДЈРНөДЛјПлАҙҪвҫцОКМвЈ®
ОӘҪвҫцЙПКцОКМвЈ¬ОТГЗ№№ҪЁИзПВКэС§ДЈРНЈә
ЈЁ1Ј©ИзНјўЩЈ¬ОТГЗҝЙТФФЪЖҪГжДЪ»ӯіц5ёцөгЈЁИОТв3ёцөг¶јІ»ФЪН¬Т»МхЦұПЯЙПЈ©Ј¬ЖдЦРГҝёцөгёчҙъұнТ»Ц§ЧгЗт¶УЈ¬БҪЦ§Зт¶УЦ®јдұИИьТ»іЎҫНУГТ»МхПЯ¶О°СЛыГЗБ¬ҪУЖрАҙЈ®УЙУЪГҝЦ§Зт¶У¶јТӘУлЖдЛыёч¶УұИИьТ»іЎЈ¬јҙГҝёцөгУлБнНв4ёцөг¶јҝЙБ¬іЙТ»МхПЯ¶ОЈ¬ХвСщТ»№ІБ¬іЙ5ЎБ4МхПЯ¶ОЈ¬¶шГҝБҪёцөгЦ®јдөДПЯ¶О¶јЦШёҙјЖЛгБЛТ»ҙОЈ¬КөјКЦ»УР МхПЯ¶ОЈ¬ЛщТФёГРЈТ»№ІТӘ°ІЕЕ іЎұИИьЈ®

ЈЁ2Ј©ИфѧУУР6Ц§ЧгЗт¶УҪшРРөҘСӯ»·ұИИьЈ¬ҪиЦъНјўЪЈ¬ОТГЗҝЙЦӘёГРЈТ»№ІТӘ°ІЕЕ__________іЎұИИьЈ»
ЎӯЎӯЎӯЎӯ
ЈЁ3Ј©ёщҫЭТФЙП№жВЙЈ¬ИфѧУУРnЦ§ЧгЗт¶УҪшРРөҘСӯ»·ұИИьЈ¬ФтёГРЈТ»№ІТӘ°ІЕЕ___________іЎұИИьЈ®
КөјКУҰУГЈә
ЈЁ4Ј©9ФВ1ИХҝӘС§КұЈ¬АПКҰОӘБЛИГИ«°аРВН¬С§»ҘПаИПК¶Ј¬Зл°аЙП42О»РВН¬С§ГҝБҪёцИЛ¶јПа»ҘОХТ»ҙОКЦЈ¬И«°аН¬С§ЧЬ№ІОХКЦ________________ҙОЈ®
НШХ№МбёЯЈә
ЈЁ5Ј©Нщ·өУЪЗаөәәНјГДПөДН¬Т»БҫёЯЛЩБРіөЈ¬ЦРНҫҫӯЗаөәұұХҫЎўО«·»ЎўЗаЦЭЎўЧНІ©4ёціөХҫЈЁГҝЦЦіөЖұЖұГж¶јУЎУРЙПіөХҫГыіЖУлПВіөХҫГыіЖЈ©Ј¬ДЗГҙФЪХв¶ОПЯВ·ЙПНщ·өРРіөЈ¬ТӘЧјұёіөЖұөДЦЦКэОӘ__________ЦЦЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
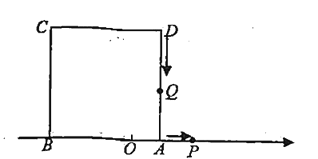
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘКэЦбЙПөг![]() ұнКҫөДКэОӘ
ұнКҫөДКэОӘ![]() ,өг
,өг![]() ұнКҫөДКэОӘ
ұнКҫөДКэОӘ![]() ,ТФ
,ТФ![]() ОӘұЯФЪКэЦбөДЙП·ҪЧчХэ·ҪРОABCD.¶Ҝөг
ОӘұЯФЪКэЦбөДЙП·ҪЧчХэ·ҪРОABCD.¶Ҝөг![]() ҙУөг
ҙУөг![]() іц·ў,ТФГҝГл
іц·ў,ТФГҝГл![]() ёцөҘО»іӨ¶ИөДЛЩ¶ИСШКэЦбХэ·ҪПтФИЛЩФЛ¶ҜЈ¬Н¬Кұ¶Ҝөг
ёцөҘО»іӨ¶ИөДЛЩ¶ИСШКэЦбХэ·ҪПтФИЛЩФЛ¶ҜЈ¬Н¬Кұ¶Ҝөг![]() ҙУөг
ҙУөг![]() іц·ў,ТФГҝГл
іц·ў,ТФГҝГл![]() ёцөҘО»іӨ¶ИөДЛЩ¶ИПтөг
ёцөҘО»іӨ¶ИөДЛЩ¶ИПтөг![]() ФИЛЩФЛ¶ҜЈ¬өҪҙп
ФИЛЩФЛ¶ҜЈ¬өҪҙп![]() өгәуФЩТФН¬СщөДЛЩ¶ИСШКэЦбХэ·ҪПтФИЛЩФЛ¶ҜЈ¬ЙиФЛ¶ҜКұјдОӘ
өгәуФЩТФН¬СщөДЛЩ¶ИСШКэЦбХэ·ҪПтФИЛЩФЛ¶ҜЈ¬ЙиФЛ¶ҜКұјдОӘ![]() Гл
Гл![]() .
.
(1)Ифөг![]() ФЪПЯ¶О
ФЪПЯ¶О![]() .ЙПФЛ¶ҜЈ¬өұtОӘәОЦөКұ,
.ЙПФЛ¶ҜЈ¬өұtОӘәОЦөКұ,![]() ?
?
(2)Ифөг![]() ФЪПЯ¶О
ФЪПЯ¶О![]() ЙПФЛ¶ҜЈ¬Б¬ҪУ
ЙПФЛ¶ҜЈ¬Б¬ҪУ![]() ,өұtОӘәОЦөКұ,ИэҪЗРО
,өұtОӘәОЦөКұ,ИэҪЗРО![]() өДГж»эөИУЪХэ·ҪРО
өДГж»эөИУЪХэ·ҪРО![]() Гж»эөД
Гж»эөД![]() ?
?
(3)ФЪөг![]() әНөг
әНөг![]() ФЛ¶ҜөД№эіМЦРЈ¬өұ
ФЛ¶ҜөД№эіМЦРЈ¬өұ![]() ОӘәОЦөКұЈ¬өг
ОӘәОЦөКұЈ¬өг![]() Улөг
Улөг![]() ЗЎәГЦШәП?
ЗЎәГЦШәП?
(4)өұөг![]() ФЪКэЦбЙПФЛ¶ҜКұЈ¬КЗ·сҙжФЪДі-КұҝМt,К№өГПЯ¶О
ФЪКэЦбЙПФЛ¶ҜКұЈ¬КЗ·сҙжФЪДі-КұҝМt,К№өГПЯ¶О![]() өДіӨОӘ
өДіӨОӘ![]() ,ИфҙжФЪЈ¬Зуіц
,ИфҙжФЪЈ¬Зуіц![]() өДЦө;ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙ.
өДЦө;ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЧЫәПУлКөјщҝОЙПЈ¬АПКҰЧйЦҜН¬С§ГЗТФЎ°ҫШРОЦҪЖ¬өДХЫөюЎұОӘЦчМвҝӘХ№КэС§»о¶Ҝ.
ЈЁ1Ј©·ЬҪшРЎЧйУГНј1ЦРөДҫШРОЦҪЖ¬ABCDЈ¬°ҙХХИзНј2ЛщКҫөД·ҪКҪЈ¬Ҫ«ҫШРОЦҪЖ¬СШ¶ФҪЗПЯACХЫөюЈ¬К№өгBВдФЪөг![]() ҙҰЈ¬Фт
ҙҰЈ¬Фт![]() Ул
Ул![]() ЦШәПІҝ·ЦөДИэҪЗРОөДАаРНКЗ________.
ЦШәПІҝ·ЦөДИэҪЗРОөДАаРНКЗ________.
ЈЁ2Ј©ЗЪѧСЧйҪ«Нј2ЦРөДЦҪЖ¬Х№ЖҪЈ¬ФЩҙОХЫөюЈ¬ИзНј3Ј¬К№өгAУлөгCЦШәПЈ¬ХЫәЫОӘEFЈ¬И»әуХ№ЖҪЈ¬ФтТФөгAЎўFЎўCЎўEОӘ¶ҘөгөДЛДұЯРОКЗКІГҙМШКвЛДұЯРОЈҝЗлЛөГчАнУЙЈ®
ЈЁ3Ј©ҙҙРВРЎЧйУГНј4ЦРөДҫШРОЦҪЖ¬ABCDҪшРРІЩЧчЈ¬ЖдЦР![]() Ј¬
Ј¬![]() Ј¬ПИСШ¶ФҪЗПЯBD¶ФХЫЈ¬өгCВдФЪөг
Ј¬ПИСШ¶ФҪЗПЯBD¶ФХЫЈ¬өгCВдФЪөг![]() өДО»ЦГЈ¬
өДО»ЦГЈ¬![]() Ҫ»ADУЪөгGЈ¬ФЩ°ҙХХИзНј5ЛщКҫөД·ҪКҪХЫөюТ»ҙОЈ¬К№өгDУлөгAЦШәПЈ¬өГХЫәЫENЈ¬ENҪ»ADУЪөгMЈ®ФтEMөДіӨОӘ________cm.
Ҫ»ADУЪөгGЈ¬ФЩ°ҙХХИзНј5ЛщКҫөД·ҪКҪХЫөюТ»ҙОЈ¬К№өгDУлөгAЦШәПЈ¬өГХЫәЫENЈ¬ENҪ»ADУЪөгMЈ®ФтEMөДіӨОӘ________cm.

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝПВБРЛө·ЁЦРЈә
ўЩФЪRtЎчABCЦРЈ¬ЎПC=90ЎгЈ¬CDОӘABұЯЙПөДЦРПЯЈ¬ИфCD=2Ј¬ФтAB=4Ј»
ўЪ°ЛұЯРОөДДЪҪЗәН¶ИКэОӘ1080ЎгЈ»
ўЫ2Ўў3Ўў4Ўў3ХвЧйКэҫЭөД·ҪІоОӘ0.5Ј»
ўЬ·ЦКҪ·ҪіМ![]() =
=![]() өДҪвОӘx=
өДҪвОӘx=![]() Ј»
Ј»
ўЭТСЦӘБвРОөДТ»ёцДЪҪЗОӘ60ЎгЈ¬Т»Мх¶ФҪЗПЯОӘ2Ј¬ФтБнТ»¶ФҪЗПЯОӘ2![]() Ј®
Ј®
ХэИ·өДРтәЕУРЈЁ Ј©
A. ўЩўЪўЫўЭ B. ўЩўЪўЫўЬ C. ўЩўЫўЬўЭ D. ўЪўЫўЬўЭ
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com