
【题目】在综合与实践课上,老师组织同学们以“矩形纸片的折叠”为主题开展数学活动.
(1)奋进小组用图1中的矩形纸片ABCD,按照如图2所示的方式,将矩形纸片沿对角线AC折叠,使点B落在点![]() 处,则
处,则![]() 与
与![]() 重合部分的三角形的类型是________.
重合部分的三角形的类型是________.
(2)勤学小组将图2中的纸片展平,再次折叠,如图3,使点A与点C重合,折痕为EF,然后展平,则以点A、F、C、E为顶点的四边形是什么特殊四边形?请说明理由.
(3)创新小组用图4中的矩形纸片ABCD进行操作,其中![]() ,
,![]() ,先沿对角线BD对折,点C落在点
,先沿对角线BD对折,点C落在点![]() 的位置,
的位置,![]() 交AD于点G,再按照如图5所示的方式折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M.则EM的长为________cm.
交AD于点G,再按照如图5所示的方式折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M.则EM的长为________cm.

【答案】(1)等腰三角形(或钝角三角形);(2)菱形,理由详见解析;(3)![]() .
.
【解析】
(1)利用折叠的性质和角平分线定义即可得出结论;
(2)利用四边相等的四边形是菱形即可得出结论;
(3)由勾股定理可求BD的长,BG的长,AG的长,利用勾股定理和折叠的性质可得到结果。
解:(1)等腰三角形(或钝角三角形).
提示:∵四边形ABCD是矩形,
∴![]() ,
,
∴![]() .
.
由折叠知,![]() ,
,
∴![]() ,
,
∴重合部分的三角形是等腰三角形.
(2)菱形.
理由:如图,
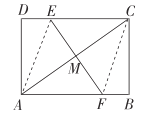
连接AE、CF,设EF与AC的交点为M,
由折叠知,![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∵四边形ABCD是矩形,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴以点A,F,C,E为顶点的四边形是菱形.
(3)![]() .
.
提示:∵点D与点A重合,得折痕EN,![]() ,
,![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴由勾股定理可得![]() ,
,
由折叠的性质可知![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,设
,设![]() ,则
,则![]() .
.
由勾股定理得![]() ,即
,即![]() ,
,
解得![]() ,即
,即![]() .
.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,OA的方向是北偏东15°,OB的方向是西偏北50°,OD是OB的反向延长线.

(1)若∠AOC=∠AOB,求OC的方向.
(2)在(1)问的条件下,作∠AOD的角平分线OE,求∠COE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】节约是中华民族的传统美德.为倡导市民节约用水的意识,某市对市民用水实行“阶梯收费”,制定了如下用水收费标准:每户每月的用水不超过![]() 立方米时,水价为每立方米
立方米时,水价为每立方米![]() 元,超过
元,超过![]() 立方米时,超过的部分按每立方米
立方米时,超过的部分按每立方米![]() 元收费.
元收费.
(1)该市某户居民9月份用水![]() 立方米(
立方米(![]() ),应交水费
),应交水费![]() 元,请你用含
元,请你用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)如果某户居民12月份交水费![]() 元,那么这个月该户居民用了多少立方米水?
元,那么这个月该户居民用了多少立方米水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .点
.点![]() 在
在![]() 轴的负半轴上,且
轴的负半轴上,且![]() 的面积为8,直线
的面积为8,直线![]() 和直线
和直线![]() 相交于点
相交于点![]() .
.
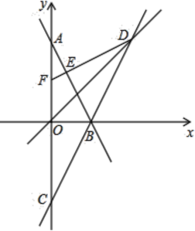
(1)求直线![]() 的解析式;
的解析式;
(2)在线段![]() 上找一点
上找一点![]() ,使得
,使得![]() ,线段
,线段![]() 与
与![]() 相交于点
相交于点![]() .
.
①求点![]() 的坐标;
的坐标;
②点![]() 在
在![]() 轴上,且
轴上,且![]() ,直接写出
,直接写出![]() 的长为 .
的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点A在x轴上,点C在y轴上,点B的坐标是![]() ,将
,将![]() 沿直线BD折叠,使得点C落在对角线OB上的点E处,折痕与OC交于点D.
沿直线BD折叠,使得点C落在对角线OB上的点E处,折痕与OC交于点D.
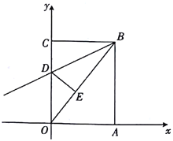
(1)求直线OB的解析式及线段OE的长.
(2)求直线BD的解析式及点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于G,F两点.若M,N分别是DG,CE的中点,则MN的长为( )

A. 3 B. 4 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
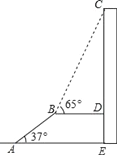
【题目】如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).
(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin65°≈
,sin65°≈![]() ,tan65°≈
,tan65°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年11月,体质监测中心有关专家随机抽查了我市若干名初中学生坐姿、站姿、走姿的好坏情况.我们对专家的测评数据作了适当处理(如果一个学生有一种以上不良姿势,我们以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请你根据图中所给信息解答下列问题:
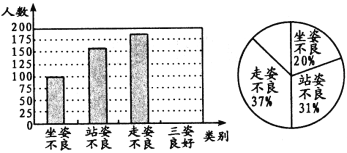
(1)请将两幅统计图补充完整;
(2)一共抽查了多少名学生?
(3)如果我市有10万名初中生,那么我市初中生中,三姿良好的学生约有多少人?
(4)根据统计结果,请你简单谈谈自己的看法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com